Loi zêta

	Zêta
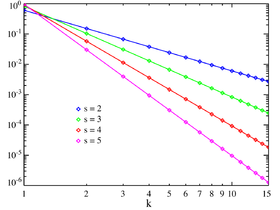	Crédit image: licence CC BY-SA 3.0 🛈 ; Fonction de masse
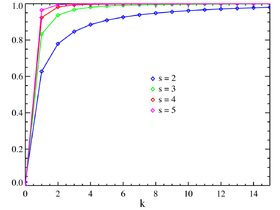	Crédit image: licence CC BY-SA 3.0 🛈 ; Fonction de répartition

En théorie de probabilité et statistiques, la distribution zêta est une loi de probabilité discrète de paramètre $s>1$ ^[1]. Elle est aussi appelée loi de Pareto discrète^[2], en lien avec la loi de Pareto.

Définition

On dit qu'une variable aléatoire $X$ suit une loi zêta de paramètre $s$ si :

$\mathbb {P} (X=k)=k^{-s}/\zeta (s)\,$

où $\zeta$ est la fonction zêta de Riemann non définie en 1^[1].

Une loi zêta est un sous cas de la loi de Zipf où le paramètre N est infini.

Moments

Le n-ième moment est défini par l'espérance de Xⁿ :

$m_{n}=\mathbb {E} (X^{n})={\frac {1}{\zeta (s)}}\sum _{k=1}^{\infty }{\frac {1}{k^{s-n}}}$

La série de droite est une représentation de la fonction zêta de Riemann et converge seulement pour les valeurs de s-n strictement supérieures à 1. Ainsi :

$m_{n}=\left\{{\begin{matrix}\zeta (s-n)/\zeta (s)&{\textrm {pour}}~n<s-1\\\infty &{\textrm {pour}}~n\geq s-1\end{matrix}}\right.$

Lien avec la densité naturelle

Soit A une partie de $\mathbb {N}$ , on dit que A a une densité naturelle si ${\frac {\operatorname {Card} (A\cap \{1,\dots ,n\})}{n}}$ converge. Notons d(A) la limite. On a alors le résultat suivant : $\mathbb {P} _{s}(X\in A){\underset {s\rightarrow 1^{+}}{\longrightarrow }}d(A)$

Démonstration

Soit $\epsilon >0$ , posons pour tout $n\in \mathbb {N} ,c_{n}=\operatorname {Card} (A\cap \{1,\dots ,n\})$ on a par hypothèse que $\lim _{n\to \infty }{\frac {c_{n}}{n}}=d(A)$ , donc on peut poser $n_{0}\in \mathbb {N}$ tel que $\forall n\in \mathbb {N} ,n\geq n_{0}\Rightarrow \left|{\frac {c_{n}}{n}}-d(A)\right|\leq \epsilon .$
On écrit alors $\mathbb {P} _{s}(X\in A)={\frac {\sum _{a\in A}{\frac {1}{a^{s}}}}{\zeta (s)}}={\frac {\sum _{\underset {a<n_{0}}{a\in A}}{\frac {1}{a^{s}}}+\sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {1}{a^{s}}}}{\zeta (s)}}$
On s'intéresse au terme $\sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {1}{a^{s}}}$ , on a : $\sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {1}{a^{s}}}=\sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {c_{a}^{s}}{c_{a}^{s}a^{s}}}\leq \sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {(d(A)+\epsilon )^{s}}{c_{a}^{s}}}$ car la variable muette a est supérieure à $n_{0}.$
Sans nuire à la généralité, supposons A infini (le cas A fini est trivial), écrivons alors $A=\{a_{0},a_{1},\dots \}$ . Il s'ensuit alors que pour $m\in \mathbb {N} ,c_{a_{m}}=m$ . posons alors $n_{1}=\operatorname {min} (\{m\in \mathbb {N} ,a_{m}\geq n_{0}\}).$
On a donc ${\frac {\sum _{\underset {a\geq n_{0}}{a\in A}}{\frac {1}{c_{a}^{s}}}}{\zeta (s)}}={\frac {\sum _{m=1}^{\infty }{\frac {1}{m^{s}}}-\sum _{m=1}^{n_{1}-1}{\frac {1}{m^{s}}}}{\zeta (s)}}={\frac {\zeta (s)-\sum _{m=1}^{n_{1}-1}{\frac {1}{m^{s}}}}{\zeta (s)}}=1-{\frac {\sum _{m=1}^{n_{1}-1}{\frac {1}{m^{s}}}}{\zeta (s)}}{\underset {s\rightarrow 1^{+}}{\longrightarrow }}1$ , d'où $\mathbb {P} _{s}(X\in A)\leq {\frac {\sum _{\underset {a<n_{0}}{a\in A}}{\frac {1}{a^{s}}}}{\zeta (s)}}+(d(A)+\epsilon )^{s}\left(1-{\frac {\sum _{m=1}^{n_{1}-1}{\frac {1}{m^{s}}}}{\zeta (s)}}\right){\underset {s\rightarrow 1^{+}}{\longrightarrow }}d(A)+\epsilon$
On fait alors de même à gauche et on trouve pour s assez proche de 1 que $d(A)-2\epsilon \leq \mathbb {P} _{s}(X\in A)\leq d(A)+2\epsilon$ , ainsi : $\mathbb {P} _{s}(X\in A){\underset {s\rightarrow 1^{+}}{\longrightarrow }}d(A)$

Voir aussi

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Zeta distribution » (voir la liste des auteurs).

↑ ^{a et b} Élise Davignon, « Introduction aux probabilités » [PDF], sur Université de Montréal
↑ « Programme probabilités discrètes » [PDF], sur université Paris Diderot

Portail des probabilités et de la statistique

Dernière mise à jour du contenu le 17/11/2023.

Droit d'auteur : le texte de l'article est disponible sous la licence CC BY-SA 3.0.
Les détails concernant les licences et crédits des images sont disponibles en cliquant sur l'image.

Le site Wikimonde est un agrégateur d'articles encyclopédiques, il n'est pas à l'origine du contenu des articles, ni des images.

Le contenu de cet article est une copie de l'article d'origine (//fr.wikipedia.org/wiki/Loi_z%C3%AAta) publié sur Wikipédia (wiki collaboratif publié sous licence libre).
Le contenu des articles n'est pas garanti.
Le texte des articles n'est pas modifié par Wikimonde. Des modifications mineures de mise en page et des liens internes (pour faciliter la navigation) peuvent être effectués automatiquement.

Des crédits concernant les images peuvent être ajoutés automatiquement selon les informations fournis par le site d'origine.
Les images sont chargées depuis des sites externes, certaines peuvent ne pas s'afficher.

Auteurs de cet article « Loi zêta » :

Lebrouillard, WikiCleanerBot, OrlodrimBot, Kelam, HB, Givet, Framabot, Florn88, FDo64, Addbot, Ethaniel, Linedwell, A2, Scrabble, Macassar, Remsirems, Lahoucine mathema, GoAskAlice, Thieol, Kondormari, Fustis, Felagoth, FenrirFinn, 2 utilisateurs non enregistrés.

[:0-1] {a et b} Élise Davignon, « Introduction aux probabilités » [PDF], sur Université de Montréal

[2] « Programme probabilités discrètes » [PDF], sur université Paris Diderot

[1]

[2]

Zêta

Crédit image: licence CC BY-SA 3.0 🛈 Fonction de masse
Crédit image: licence CC BY-SA 3.0 🛈 Fonction de répartition