Test de normalité
En statistiques, les tests de normalité permettent de vérifier si des données réelles suivent une loi normale ou non. Les tests de normalité sont des cas particuliers des tests d'adéquation (ou tests d'ajustement, tests permettant de comparer des distributions), appliqués à une loi normale.
L'usage de ces tests est très controversés en statistiques. En effet, un test statistique est conçu pour rejeter l'hypothèse nulle. Or, ces tests sont généralement utilisés pour "prouver" qu'une distribution est normale, c'est-à-dire pour accepter l'hypothèse nulle, ce qui par définition même d'un test statistique est une erreur conceptuelle.
Intuitivement, cela se conçoit très bien : sur une variable qui a un effectif particulièrement faible, un test de normalité manquera de puissance et il ne rejettera pas l'hypothèse nulle, même si la loi que suit la variable n'est pas du tout normale. Or, dans le cas ou l'on veut décider si on doit appliquer un test paramétrique ou non paramétrique, c'est justement sur les variables à faible effectif qui est primordial qu'une variable suive une loi normale. Autrement dit, c'est justement quand on a besoin du test de normalité qu'il est le moins efficace.
Approches empiriques et graphiques
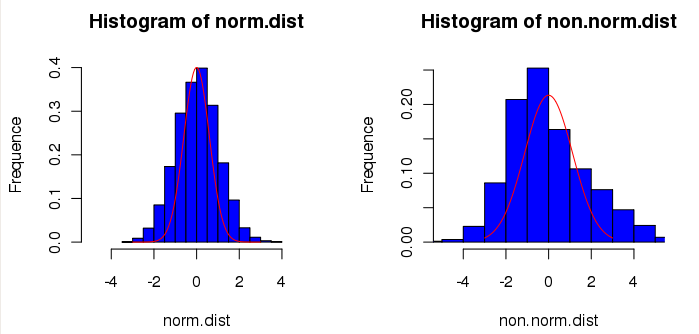
Histogramme de la distribution
Il est possible de visualiser la forme de la distribution des données à analyser en les représentant sous forme d'histogramme puis de comparer la forme de cet histogramme avec une courbe représentant une loi normale (les paramètres de cette loi étant calculés à partir des données à analyser, voir Théorème central limite). Ceci ne permet pas de conclure à la normalité des données mais peut donner une idée du type de loi sous-jacente. Par exemple une loi normale, ou loi de Student si la distribution semble symétrique, loi log-normale, loi gamma, loi de Weibull, loi exponentielle ou loi bêta si la distribution est asymétrique.
Histogramme des résidus
Il est également possible de représenter l'histogramme des résidus (c'est-à-dire la différence entre la distribution observée et la loi normale). Les résidus doivent suivre également une loi normale.
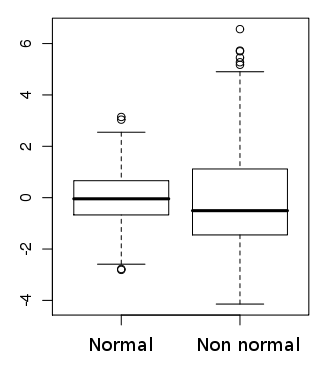
Boîte à moustaches (box-plot)
Une boîte à moustaches permet de visualiser rapidement la symétrie de la distribution des données réelles et la présence de valeurs atypiques.
Graphe quantile-quantile (qq-plot)
On peut représenter l'adéquation à une loi normale visuellement en se rapprochant d'un modèle linéaire par calcul des quantiles. On a pour cela la méthode de la droite de Henry, qui permet de comparer les valeurs des quantiles des valeurs empiriques centrées réduites aux quantiles de la loi normale centrée réduite .
Coefficients d'asymétrie et d'aplatissement
Les coefficients d'asymétrie et d'aplatissement (correspondant respectivement aux moments d'ordre 3 et 4) sont également utiles pour définir une loi normale.
- pour l'aplatissement :
- pour l'asymétrie :
avec la racine d'un estimateur non biaisé de la variance.
On sait effectivement que le coefficient d'asymétrie vaut zéro pour toute loi normale, tandis que le coefficient d'aplatissement vaut 3 (0 si normalisé)
Approche probabiliste
Il existe également un grand nombre de tests de normalité :
- Tests basés sur la fonction de répartition empirique : Test de Kolmogorov-Smirnov et son adaptation le test de Lilliefors, ou le test de Anderson-Darling et le test de Cramer-Von Mises
- Tests basés sur les moments, comme le Test de Jarque-Bera ou le test de D'Agostino.
- ou encore le test de Shapiro-Wilk, ou le test de Shapiro–Francia.
Un article de 2011 du Journal of Statistical Modeling and Analytics[1] conclut que Shapiro-Wilk a la meilleure puissance pour un niveau de signifiance donné, suivi de près par Anderson-Darling, en comparant les tests de Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors, et Anderson-Darling.
Généralités
Les tests de normalité sont des tests d'hypothèse. En notant la fonction de répartition basée sur les données à analyser et la fonction de répartition théorique, les hypothèses nulle et alternative peuvent s'écrire :
.
Les tests sur les moments ont une hypothèse moins forte, ils ne testent pas si la fonction de répartition est normale, mais si les moments (coefficients d'asymétrie et d'aplatissement) de la distribution inconnue sont identiques à ceux d'une loi normale:
On remarquera que ce n'est pas suffisant pour caractériser une loi normale (Problème des moments).
Test d'adéquation du χ²
Son utilisation n'est pas recommandée du fait de son manque de puissance et de la nécessité de diviser les distributions en classes[2].
Tests bayesiens
Applications
Une application des tests de normalité concerne les résidus d’un modèle de régression linéaire. S’il ne sont pas distribués de façon normale, les résidus ne peuvent pas être utilisés dans des tests Z ou dans quelqu’autre test que ce soit, à partir du moment où il fait intervenir des hypothèses de normalité (par exemple, le test t, le test de Fisher ou le test du χ²). Si les résidus ne sont pas normalement distribués, cela signifie que la variable dépendante, ou tout au moins une variable explicative, pourrait avoir une fonction de répartition erronée ; des variables importantes peuvent également être manquantes. Une ou plusieurs correction de ces erreurs classiques peuvent engendrer des résidus qui suivent une distribution normale.
Voir aussi
- Gilbert Saporta, Probabilités, Analyse des données et Statistiques, Paris, Éditions Technip, , 622 p. [détail des éditions] (ISBN 978-2-7108-0814-5, présentation en ligne) (p. 359 à 370).
- Judge et al., Introduction to the Theory and Practice of Econometrics, Second Édition, 1988; 890–892.
- Gujarati, Damodar N., Basic Econometrics, Fourth Édition, 2003; 147–148









