Loi hypo-exponentielle

Loi hypo-exponentielle
Crédit image: Ipipipourax licence CC BY-SA 3.0 🛈 Densité de probabilité
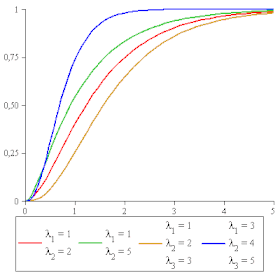
Crédit image: Ipipipourax licence CC BY-SA 3.0 🛈 Fonction de répartition
Paramètres	n=1,2,... ${\displaystyle \lambda _{i}>0}$
Support	${\displaystyle x\in [0;\infty [\!}$
Densité de probabilité	${\displaystyle \sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\lambda _{i}\mathrm {e} ^{-\lambda _{i}x}}$
Fonction de répartition	${\displaystyle 1-\sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\mathrm {e} ^{-\lambda _{i}x}}$
Espérance	${\displaystyle \sum _{i=1}^{k}1/\lambda _{i}\,}$
Médiane	${\displaystyle \ln(2)\sum _{i=1}^{k}1/\lambda _{i}\,}$
Variance	${\displaystyle \sum _{i=1}^{k}1/\lambda _{i}^{2}}$
Asymétrie	${\displaystyle \sum _{i=1}^{n}{\frac {1}{\lambda _{i}^{2}}}}$

En théorie des probabilités et en statistique, la loi hypo-exponentielle ou loi d'Erlang généralisée^[1] est une loi de probabilité continue, à support semi-infini qui trouve des applications dans les mêmes domaines que la loi d'Erlang : théorie des files d'attente, ingénierie de trafic, etc. Le terme hypo vient du fait que le coefficient de variation de la loi est inférieur à un, comparativement à la loi hyper-exponentielle dont le coefficient de variation est supérieur à un et à la loi exponentielle dont le coefficient vaut un.

Une variable aléatoire qui suit une loi hypo-exponentielle sera notée : ${\displaystyle Y\sim \mathrm {Hypo} (\lambda _{1},\dots ,\lambda _{n})}$.

La loi hypo-exponentielle définie comme la loi de la somme de n variables aléatoires ${\textstyle X_{i},\,i=1,\dots ,n}$ de loi exponentielle indépendantes de paramètres respectifs : ${\textstyle \lambda _{i},\,i=1,\dots ,n}$ :

${\displaystyle Y=\sum _{i=1}^{n}X_{i}}$ avec ${\displaystyle X_{i}\sim {\mathcal {E}}(\lambda _{i})}$.

Le coefficient de variation minimum de la loi hypo-exponentielle est ${\displaystyle 1/n}$.

Dans le cas où les paramètres ${\textstyle \lambda _{i}}$ sont tous distincts, la densité de probabilité de la loi hypo-exponentielle se calcule par récurrence^[2] pour obtenir la formule :

${\displaystyle f_{X}(x)={\begin{cases}\displaystyle \sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\lambda _{i}\mathrm {e} ^{-\lambda _{i}x}&{\text{ si }}x>0\\0&{\text{ sinon }}\end{cases}}}$

La fonction de répartition de la loi hypo-exponentielle est donnée par^[2] :

${\displaystyle F_{X}(x)={\begin{cases}\displaystyle 1-\sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\mathrm {e} ^{-\lambda _{i}x}&{\text{ si }}x>0\\0&{\text{ sinon }}\end{cases}}}$

avec le même critère pour le paramètres ${\textstyle \lambda _{i}\;:\;\lambda _{i}\neq \lambda _{j},{\text{ si }}i\neq j}$.

• Portail des probabilités et de la statistique