Histogramme
| Type |
Représentation graphique de données statistiques (en), diagramme à barres |
|---|---|
| Décrit par |
ISO 3534-1:2006(en) Statistics — Vocabulary and symbols — Part 1: General statistical terms and terms used in probability () |
| Aspect de |


En statistique, un histogramme est une représentation graphique permettant de représenter la répartition empirique d'une variable aléatoire ou d'une série statistique en la représentant avec des colonnes correspondant chacune à une classe et dont l'aire est proportionnelle à l'effectif de la classe[1].
Un outil d'exploration des données
L’histogramme est un moyen rapide pour étudier la répartition d’une variable. Il peut être, en particulier utilisé en gestion de la qualité lorsque les données sont obtenues lors d’une fabrication.
Exemples :
- diamètre d’un arbre après usinage ;
- dureté d’une série de pièces après un traitement thermique ;
- concentration d’un élément dans la composition d’alliages produit par une fonderie ;
- masse de préparation alimentaire dans une boîte de conserve ;
- répartition de la luminosité des pixels dans une photographie.
L’histogramme est un outil « visuel » qui permet de détecter certaines anomalies ou de faire un diagnostic avant d’engager une démarche d’amélioration. Utilisé dans ce cadre, l’histogramme est un outil « qualitatif ». Pour pouvoir bien mener l’étude de la dispersion d’une variable à l’aide d’un ou de plusieurs histogrammes, il faut avoir une bonne connaissance de la variable étudiée. De même, il faut connaître les conditions de collecte des données : fréquence de mesure, outil de mesure utilisé, possibilité de mélange de lots, possibilité de tri etc.
Construction
Collecte des données
La première phase est la collecte des données en cours de fabrication. Cette collecte peut être réalisée soit de façon exceptionnelle à l’occasion de l’étude de la variable soit en utilisant un relevé automatique ou manuel fait lors d’un contrôle réalisé dans le cadre de la surveillance du procédé de fabrication.
Sans qu’il soit réellement possible de donner un nombre minimum, il faut que le nombre de valeurs relevées soit suffisant. Plus on dispose d’un nombre élevé de valeurs, plus l’interprétation sera aisée.
Nombre de classes
Le choix des classes, soit leur nombre et leurs largeurs, n'est pas univoque. Il convient pour les déterminer de prendre en compte à la fois la nature de la distribution et le nombre de points de données. Souvent, dans le cadre d’une analyse de ce type, on utilise des classes de largeur identique.
On pourra trouver dans la littérature de nombreuses suggestions de choix pour le nombre de classes. Citons par exemple :
- Celle de Herbert Sturges (1926)[2] qui, pour N points de données répartis avec une distribution approximativement normale, suggère un nombre de classes K obtenu avec la formule suivante [3] :
- .
On pourra consulter utilement l'article Règle de Sturges à ce propos.
- L'alternative à la règle précédente est la règle dite de Rule [4] où
- .
- Le choix simple de la racine carrée :
- .
En tout état de cause, l’histogramme étant un outil visuel, il est possible de faire varier le nombre de classes. Ceci permet de voir l’histogramme avec un nombre différent de classes et ainsi de trouver le meilleur compromis qui facilitera l’interprétation. L’utilisation d’un logiciel dédié ou plus simplement d’un tableur facilite cette opération.
Intervalles de classe
L’amplitude (minimale) w de l’histogramme est
Il peut cependant être intéressant pour obtenir un histogramme plus parlant de choisir une amplitude plus large que l'amplitude minimale.
L’amplitude h théorique de chaque classe est alors :
Il faut arrondir cette valeur à un multiple de résolution de l’instrument de mesure (arrondi à l'excès).
Exemple : Soit la masse d’une préparation culinaire avant conditionnement. Le calcul d'amplitude de classe donne hth = 0,014 kg. La résolution de la balance utilisée est de 0,001 kg. On arrondit la valeur h à 0,015 kg.
Les classes peuvent être du type [limite inférieure ; limite supérieure[ ou ] limite inférieure ; limite supérieure].
La valeur minimale de la première classe est donnée par la valeur minimale de la série moins une demi-résolution.
Exemple : la valeur la plus petite relevée lors de la fabrication de la préparation culinaire est de 0,498 kg. La limite inférieure sera: 0,498 – (0,001 / 2) = 0,497 5 kg.
Pour plus de facilité, il est préférable de prendre une valeur « ronde », par exemple 0,495 kg.
Hauteur des rectangles
Pour un exemple développé in extenso, voir article : Statistiques élémentaires continues Plusieurs choix sont possibles pour déterminer la hauteur des rectangles.
- Les hauteurs correspondent aux effectifs, soit pour chaque rectangle le nombre d'observations dans la classe correspondante.
- Les hauteurs correspondent aux fréquences, soit pour chaque rectangle la proportion, donnée par exemple en pourcentage, d'observations dans la classe correspondante.
- Les hauteurs sont déterminées de manière que la surface du rectangle corresponde à la fréquence relative d'observations dans la classe correspondante.
La troisième méthode permet en outre d'accommoder des classes de largeur variable ce qui est utile lorsque les données sont peu denses dans certaines régions.
Exemple
Soit la fabrication de rations alimentaires, la pesée des rations avant emballage donne la série de mesures suivantes en kg :
| 0,547 | 0,563 | 0,532 | 0,521 | 0,514 | 0,547 | 0,578 | 0,532 | 0,552 | 0,526 | 0,534 | 0,560 | 0,502 | 0,503 | 0,516 | 0,565 |
| 0,532 | 0,574 | 0,521 | 0,523 | 0,542 | 0,539 | 0,543 | 0,548 | 0,565 | 0,569 | 0,574 | 0,596 | 0,547 | 0,578 | 0,532 | 0,552 |
| 0,554 | 0,596 | 0,529 | 0,555 | 0,559 | 0,503 | 0,499 | 0,526 | 0,551 | 0,589 | 0,588 | 0,568 | 0,564 | 0,568 | 0,556 | 0,523 |
| 0,526 | 0,579 | 0,551 | 0,584 | 0,551 | 0,512 | 0,536 | 0,567 | 0,512 | 0,553 | 0,534 | 0,559 | 0,498 | 0,567 | 0,589 | 0,579 |
Les caractéristiques du relevé sont les suivantes :
- nombre d'échantillons : N=64 ;
- étendue : w=0,098 kg ;
- valeur minimale : 0,498 kg ;
- Valeur maximale : 0,596 kg.
On en déduit les paramètres suivants pour l'histogramme :
- le nombre de classes est de 7 (en utilisant la formule avec le logarithme) ;
- l'amplitude de classe est 0,098/7 = 0,014 kg que l'on arrondit à 0,015 kg (résolution de la balance : 0,001 kg) ;
- la valeur minimale de la première classe est de 0,498 – (0,001/2) = 0,4975. Par souci de facilité pour l'interprétation, on peut arrondir cette valeur à 0,495 kg.
On obtient l'histogramme suivant :
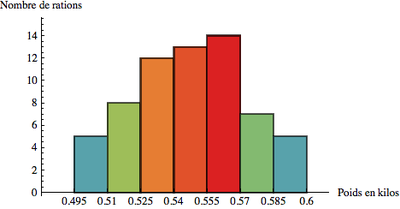
Interprétation

La distribution de beaucoup de paramètres industriels correspond souvent à une loi normale. On compare souvent l'histogramme obtenu au profil « en cloche » de la loi normale. Cette comparaison est visuelle et même si elle peut être une première approche, elle ne constitue pas un test de « normalité ». Pour cela, il faut exécuter un test dont un des plus classiques est la droite de Henry.
La distribution suivant la loi normale, si elle est extrêmement fréquente, n'est pas systématique. On vérifiera que la distribution ne correspond pas à une distribution de défaut de forme (exemple : mesure de l'excentration dans un tube, position d'objets lancés dans la direction d'un mur dont certains rebondissent sur ce mur).
L'interprétation peut, par exemple, donner les résultats suivants :
| Histogramme montrant un mélange de deux lots. | Histogramme montrant un mélange de deux lots mais avec une moyenne proche. On veillera dans ce cas à faire aussi varier le nombre de classes pour vérifier qu'il ne s'agit pas d'un problème de construction. | Histogramme montrant que le lot a subi un tri. Tous les éléments pour lesquels la valeur du paramètre mesuré était inférieure à A ont été supprimés. |
 Crédit image: L’auteur n’a pas pu être identifié automatiquement. Il est supposé qu'il s'agit de : Romary (étant donné la revendication de droit d’auteur). licence CC BY 2.5 🛈 |
 Crédit image: L’auteur n’a pas pu être identifié automatiquement. Il est supposé qu'il s'agit de : Romary (étant donné la revendication de droit d’auteur). licence CC BY 2.5 🛈 |
 Crédit image: L’auteur n’a pas pu être identifié automatiquement. Il est supposé qu'il s'agit de : Romary (étant donné la revendication de droit d’auteur). licence CC BY 2.5 🛈 |
Dans le cas d'histogramme montrant un mélange de deux lots ayant une moyenne différente, il existe des cas où la dispersion présente cet aspect sans pour autant incriminer un mélange. C'est par exemple le cas de la mesure d'une pièce cylindrique mais qui présente un défaut de type ovalisation. Les deux moyennes représentent alors le grand diamètre et le petit diamètre. C'est la connaissance du procédé et/ou du produit qui permet de réaliser ce type d'interprétation.
Un outil pour estimer une densité
Dans cette section, on utilise l'histogramme non pas comme un outil de visualisation, mais comme une estimation statistique de la distribution sous-jacente de l'échantillon. On dispose d'un échantillon indépendamment et identiquement distribué selon une loi. On souhaite déduire de l'échantillon une estimation de la densité inconnue, notée f.
Le cas discret
On recherche les probabilités qui caractérisent la distribution. On note cette distribution f par abus. Un estimateur naturel est :
où est le nombre d'observations de l'échantillon qui sont égales à x. Une manière alternative de noter cet estimateur est :
où est la fonction indicatrice : elle vaut 1 lorsque son argument est vrai.
Le cas continu
L'estimateur précédent n'est plus valable, car dans le cas continu, on ne peut plus compter le nombre d'observations exactement égales à x. Par contre, on peut considérer une boîte centrée en x, et de largeur h, paramètre positif. On peut compter le nombre d'observations approximativement (et non plus exactement) égales à x, en comptant les observations tombant dans ladite boîte. L'estimateur[5] devient :
ou encore, en posant :
- .
Le paramètre h contrôle le niveau de lissage de l'estimation et doit être recherché avec soin. L'estimateur précédent présente de bonnes propriétés comparables à celles d'une densité continue:
- il est positif ;
- il s'intègre à l'unité.
Toutefois, il présente un gros défaut pour pouvoir estimer une densité : il n'est pas continu. Pour gagner la continuité, on utilisera l'estimateur de Parzen (ou à noyau). Le principe est simple : il suffit de remplacer la fonction indicatrice par une fonction réelle, qui attribue un poids d'autant plus important que les observations sont situées à proximité de x. À titre d'exemple voici deux estimations de densité par la méthode des noyaux avec des paramètres différents :
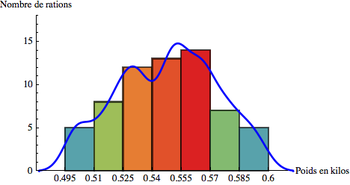

Origine
William Playfair (Commercial and political atlas, 1786) est le premier promoteur de l'exploitation des observations statistiques par des courbes de distribution et des diagrammes en bâtons. Le mot histogramme a été proposé par Pearson en 1895.
Notes et références
- ↑ « Histogramme », sur [email protected]
- ↑ (en) Herbert Sturges, « The choice of a class-interval », J. Amer. Statist. Assoc., no 21, , p. 65-66
- ↑ Maurice Pillet, Appliquer la maîtrise statistique des procédés MSP/SPC, Les Éditions d'Organisation, 1995
- ↑ Online Statistics Education: A Multimedia Course of Study (http://onlinestatbook.com/). Project Leader: David M. Lane, Rice University (chapter 2 "Graphing Distributions", section "Histograms")
- ↑ Fix, E., Hodges Jr., J., 1951. Discriminatory analysis: non-parametric discrimination: Consistency properties. Report No. 4, USAF School of Aviation Medicine, Randolph Field, TX.
Voir aussi
Bibliographie
- Maurice Lethielleux, Statistique descriptive, Paris, , 124 p. (ISBN 2 10 003513 4).
- Maurice Pillet, Appliquer la maîtrise statistique des procédés MSP/SPC, Les Éditions d'Organisation, , 336 p. (ISBN 2-7081-1774-2).
- Pierre Souvay, Statistique et qualité, Paris, AFNOR, coll. « À savoir », , 40 p..
- Pierre Souvay, Savoir utiliser la statistique, outil à la décision et à l'amélioration de la qualité, Saint-Denis-la-Plaine, AFNOR, , 434 p. (ISBN 2-12-475821-7).















