Puissance (physique)

Puissance

Crédit image:

Eric Magnan

licence CC BY-SA 3.0 🛈

Détecteur associé à un puissance-mètre pour laser.

Données clés

Unités SI	watt
Autres unités	cheval-vapeur
Dimension	M·L 2·T −3
Nature	Grandeur scalaire extensive
Symbole usuel	P
Lien à d'autres grandeurs	P = ${\displaystyle {\partial \over \partial t}}$W
Conjuguée	temps (physique)

En physique, la puissance est la quantité d'énergie par unité de temps fournie par un système à un autre. C'est donc une grandeur scalaire. La puissance correspond à un débit d'énergie : si deux systèmes de puissances différentes fournissent le même travail, le plus puissant des deux est celui qui le fournit le plus rapidement.

D'une façon générale, l'intégrale de la puissance P fournie pendant une durée τ représente l'énergie totale fournie :

${\displaystyle W=\int _{0}^{\tau }{\mathcal {P}}(t)\,\mathrm {d} t}$.

Lorsque la puissance P est constante, la capacité d'un système à fournir un travail W au cours d'une durée Δt s'exprime alors par le rapport :

${\displaystyle {\mathcal {P}}={\frac {W}{\Delta t}}}$.

Dans le système international d'unités, une puissance s'exprime en watts, qui correspondent à des joules par seconde, ou de façon équivalente à des kg.m² .s⁻³. Ainsi, 1 W = 1 J s⁻¹ = 1 kg m² s⁻³. Une unité ancienne était le cheval-vapeur, par lequel la capacité de traction d'une machine à vapeur était comparée à celle d'un cheval de trait.

En tant que grandeur physique, la puissance reflète à la fois la notion de changement matériel dans l'Univers et celle de temps nécessaire à effectuer ce changement. La puissance se distingue en cela du travail, qui ne prend en compte que le changement, mais non la durée nécessaire.

Ainsi, lorsqu'une charge pesante est transportée en haut d'un escalier, le même travail est effectué que le porteur le fasse en marchant ou en courant ; mais la puissance nécessaire dans ce second cas est beaucoup plus grande, car le délai d'accomplissement de ce travail est plus faible.

Un autre exemple paradoxal est que la « combustion complète » d'un kilogramme de charbon produit plus d'énergie que l'explosion d'un kilogramme de TNT : brûler du charbon produit de l'ordre de 15 à 30 mégajoules par kilogramme^[1], tandis que l'explosion de TNT produit à peu près 4,7 MJ kg^{−1 [note 1]}. La différence essentielle est en fait une différence de puissance : l'explosion du TNT étant beaucoup plus rapide que la combustion du charbon, la puissance du TNT est bien supérieure à celle du charbon à poids égal, bien que l'énergie intrinsèque du charbon soit supérieure à celle du TNT.

D'une manière générale, la puissance est le produit d'une « variable d'effort » (force, couple, pression, tension, etc.) nécessaire à la mise en mouvement contre la résistance du système, par une « variable de flux » (vitesse, vitesse angulaire, débit, intensité du courant, etc.) entretenu malgré cette résistance.

Ainsi, la puissance nécessaire pour imposer un déplacement à un véhicule est le produit de la force de traction exercée par la vitesse de déplacement. La puissance d'un moteur rotatif est le produit du couple qu'il transmet par la vitesse de rotation qu'il est capable d'entretenir malgré cette résistance. Une ampoule électrique convertit de l'énergie électrique en lumière et en chaleur, et la puissance ainsi consommée est le produit de la tension électrique par l'intensité du courant électrique qui la traverse^[2],[3].

La puissance moyenne

La puissance moyenne P_m est l'énergie E délivrée par un phénomène divisée par la durée τ de ce phénomène, soit ${\displaystyle {\mathcal {P}}_{m}={\frac {E}{\tau }}}$.

La puissance instantanée

La puissance instantanée est la dérivée de l'énergie fournie par rapport au temps, soit ${\displaystyle {\mathcal {P}}(t)={\frac {\mathrm {d} E}{\mathrm {d} t}}}$ d'où ${\displaystyle {\mathcal {P}}_{m}=\langle {\mathcal {P}}(t)\rangle ={\frac {1}{\tau }}\int _{0}^{\tau }{\mathcal {P}}(t)\,\mathrm {d} t}$.

Crédit image:

A7N8X

licence CC BY-SA 3.0 🛈

Dans certains cas, il faut une grande puissance au démarrage (grande énergie sur une courte durée) pour mettre le système en mouvement, mais une fois le système mis en mouvement, il suffit d'une faible puissance pour entretenir le mouvement. En effet, au départ, la puissance doit combattre toute l'inertie du système ; alors qu'en régime continu, il n'y a plus qu'à compenser l'élément dissipatif dû généralement aux frottements. C'est notamment le cas lorsqu'il faut vaincre un frottement sec, une force d'inertie, ou en cas d'effet de seuil (exemples : la vitesse minimale de décollage d'un avion ou d'une fusée).

Par exemple :

• une péniche tirée par un cheval sur un chemin de halage demande, au départ, un très grand effort, afin de vaincre la force d'inertie, avant d'obtenir un déplacement sensible. Ensuite, il peut avancer au pas, sans s'épuiser, le long du canal ;
• une rame de métro consomme une puissance d'environ un mégawatt pour se lancer, et 10 à 15 fois moins pour maintenir sa vitesse de croisière.

Pour cette raison, la puissance motrice doit alors être surdimensionnée par rapport au strict besoin résultant de la vitesse de croisière ; et inversement, la conduite du système doit prévoir de réduire la puissance après démarrage, afin de ne pas emporter le système au-delà de son régime de fonctionnement normal.

D'autre part, la puissance fournie est donc le produit d'une variable d'effort par une variable de flux, y compris au démarrage d'un système. Si donc au démarrage on impose au système toute la puissance disponible à sa valeur nominale, la « variable d'effort » devra théoriquement prendre une valeur infinie, pour compenser une « variable de flux » initialement nulle. De ce fait, en pratique, la puissance transmise à un système au repos ne peut qu'augmenter progressivement. Mais inversement, une montée en puissance trop rapide peut imposer à la « variable d'effort » un pic instantané sous forme de choc, susceptible de détériorer le système.

L'unité de puissance du SI est le watt (symbole : W), qui correspond à un joule par seconde.

Curieusement, on utilise encore le cheval-vapeur dans le cas des moteurs thermiques :

1 ch = 736 W environ.

Par abus de langage, on attribue la puissance à l'objet qui la transforme, par exemple :

• un moteur de 100 ch ;
• une lampe de 100 W.

Dans ce cas il peut s'agir de :

• la puissance maximale (moteur à plein régime, ou à régime donné) ;
• la puissance nominale sous condition de fonctionnement (par exemple lampe à incandescence alimentée en 230 V).

Le principe des puissances virtuelles, fondamental en mécanique, met sous forme variationnelle les équations traditionnelles de la mécanique. Il permet aussi d'établir des relations entre les puissances extérieures d'un mécanisme (et donc d'obtenir des lois entrée/sortie par exemple).

Puissance des interactions

En particulier, dans une liaison parfaite, la puissance des interactions est nulle. On obtient cette grandeur par le calcul du co-moment des torseurs cinématique et statique de la liaison.

Puissance d'une force

La puissance mécanique d'une force est l'énergie que l'on peut acquérir ou perdre avec cette force sur un temps donné.

Si le point d'application d'une force ${\displaystyle {\vec {F}}}$ (en newtons) se déplace à la vitesse instantanée ${\displaystyle {\vec {v}}}$ (en m/s), alors la puissance instantanée vaut (en watts) :

${\displaystyle {\mathcal {P}}={\vec {F}}\cdot {\vec {v}}}$.

On retrouve aisément ce résultat en dérivant le travail d'une force.

Puissance d'un couple

Si l'objet est en rotation sous l'action d'un couple ${\displaystyle {\vec {C}}}$ (en newton mètres) et tourne à la vitesse angulaire instantanée ${\displaystyle {\vec {\omega }}}$ (en radians par seconde), alors la puissance instantanée vaut (en watts) : ${\displaystyle {\mathcal {P}}={\vec {C}}\cdot {\vec {\omega }}}$.

Puissance des torseurs

La puissance électrique que l'on note souvent P et qui a pour unité le watt (symbole W) est le produit de la tension électrique aux bornes de laquelle est branchée l'appareil (en volts) et de l'intensité du courant électrique qui le traverse (en ampères) pour des appareils purement résistifs.

Crédit image:

licence CC BY-SA 3.0 🛈

En régime de tension et de courant continu, ${\displaystyle {\mathcal {P}}=U\,I}$ avec U et I les valeurs constantes de la tension aux bornes du dipôle et de l'intensité du courant à travers le dipôle.

En particulier, si R est la résistance d'un dipôle, alors on a :

${\displaystyle U=R\,I}$.

Cela conduit à l'expression de la puissance :

${\displaystyle {\mathcal {P}}=R\,I^{2}={\frac {U^{2}}{R}}}$.

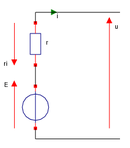
D'un point de vue électrique, on peut modéliser un dipôle actif linéaire (électromoteur) par un Modèle équivalent de Thévenin (MET). Remarque : ce modèle est très sommaire et ne rend compte que de la chute de tension en charge ou des puissances électriques mises en jeu que dans un domaine de validité qui doit toujours être précisé. En convention générateur (flèche de tension et sens du courant dans le même sens), le schéma équivalent du dipôle est donc le suivant :

En convention générateur, la puissance fournie par le dipôle à l'extérieur s'écrit par définition :

${\displaystyle {\mathcal {P}}_{\mathrm {fournie} }=U\,I=(E-r\,I)\,I=E\,I-r\,I^{2}}$.

La puissance fournie P_fournie par le dipôle actif correspond donc à la puissance fournie par un générateur idéal de tension E délivrant un courant I dont une partie, ${\displaystyle -r\,I^{2}}$, est dissipée par effet Joule. Dans le cas des moteurs électriques, le terme EI est appelé puissance électromécanique et souvent noté ${\displaystyle {\mathcal {P}}_{\mathrm {em} }}$.

Si la tension et le courant varient, la puissance instantanée consommée par un dipôle est égale au produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes.

${\displaystyle p(t)=u(t)\,i(t)}$

avec : p en watts, u en volts et i en ampères.

Crédit image:

Original téléversé par P.loos sur Wikipédia français.

licence CC BY-SA 3.0 🛈

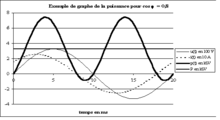
En régime sinusoïdal, le courant et la tension ont pour expression :

${\displaystyle i(t)=I_{0}\,\cos(\omega \,t)=I_{\mathrm {eff} }\,{\sqrt {2}}\,\cos(\omega \,t)}$

${\displaystyle u(t)=U_{0}\,\cos(\omega \,t+\varphi )=U_{\mathrm {eff} }\,{\sqrt {2}}\,\cos(\omega \,t+\varphi )}$

où U_eff et I_eff sont les valeurs efficaces de la tension et du courant, et φ est le déphasage de la tension par rapport au courant.

Le produit de ces deux grandeurs a pour expression :

${\displaystyle p(t)=U_{\mathrm {eff} }\,I_{\mathrm {eff} }\,\cos \varphi +U_{\mathrm {eff} }\,I_{\mathrm {eff} }\,\cos(2\,\omega \,t+\varphi ).}$

La moyenne de puissance instantanée, appelée puissance active, correspond à la puissance réellement consommée par le dipôle. Le second terme de la somme correspond à la puissance fluctuante.

La puissance active vaut :

${\displaystyle {\mathcal {P}}=\langle p(t)\rangle =U_{\mathrm {eff} }\,I_{\mathrm {eff} }\,\cos \varphi }$

où cos(φ) est le facteur de puissance.

La « puissance fluctuante » est une puissance sinusoïdale de fréquence double de celle du courant et de la tension. Pour des convertisseurs électrothermiques, cette puissance fluctuante n'a aucun effet, l'inertie thermique du système permettant de lisser totalement ces variations de puissance. En revanche, lors d'une conversion électromécanique, la machine électrique, moteur ou génératrice, du fait de son inertie, tourne avec une vitesse mécanique quasi constante et, à chaque instant, elle consomme ou fournit — aux pertes près — une puissance mécanique identique. La puissance fluctuante est alors responsable d'oscillations de couples qui sont, en majeure partie, absorbées par l'élasticité de l'arbre de transmission. Pour une machine de forte puissance, ces oscillations sont rédhibitoires car elles pourraient provoquer sa destruction. C'est une des raisons pour lesquelles les alternateurs des centrales électriques et les très gros moteurs doivent être polyphasés et sont, le plus souvent, des machines triphasées.

La puissance thermique (ou puissance de chauffage) est la quantité de chaleur (ou transfert thermique) traversant une surface isotherme par unité de temps. Il s'agit donc d'un flux de chaleur qui s'exprime en watts (et ses multiples : kilowatts, mégawatts...), la quantité de chaleur étant exprimée en joules et le temps en secondes. D'autres unités, devenues obsolètes, sont la kilocalorie par heure (kcal/h) et la thermie par heure (th/h).

Par exemple, la puissance thermique d'un radiateur est de l'ordre de 1 000 watts (1 kW), tandis que celle d'un réacteur nucléaire peut atteindre plus de 1 000 MW (1 GW).

D'après le premier principe de la thermodynamique, la puissance thermique et la puissance mécanique sont équivalentes. D'après le second principe de la thermodynamique, la transformation de puissance thermique en puissance mécanique n'est pas intégrale, il y a toujours une puissance thermique dissipée. La puissance thermique s'écoule toujours des régions les plus chaudes vers les régions les plus froides.

Dans le cas d'un transfert thermique par conduction, on introduit de manière unidimensionnelle la densité de flux thermique :

${\displaystyle \varphi =-\lambda \,{\frac {\partial T}{\partial x}}}$.

La loi de Fourier généralise cette densité de flux dans toutes les directions. Le vecteur densité de flux thermique est défini par :

${\displaystyle {\vec {\jmath }}_{Q}=-\lambda \;{\overrightarrow {\mathrm {grad} }}\,T}$.

Cette expression de la propagation de chaleur présente deux avantages :

• elle est tridimensionnelle (elle exprime la propagation dans toutes les directions de l'espace) ;
• on peut librement utiliser les coordonnées de notre choix (cartésiennes, cylindriques ou sphériques).

Le choix des coordonnées dépend de la symétrie du problème. Par exemple, pour étudier la chaleur produite par un fusible (cylindrique), on utilise les coordonnées cylindriques^{[note 2]}.

La puissance thermique (notée P_Q) à travers une surface S^{[note 3]} est par définition, le flux du vecteur ${\displaystyle {\vec {\jmath }}_{Q}}$ à travers la surface S, c'est-à-dire :

${\displaystyle {\mathcal {P}}_{Q}=\iint \limits _{S}{\vec {\jmath }}_{Q}\cdot \mathrm {d} {\vec {S}}}$.

La puissance acoustique, ou puissance sonore, est la quantité d'énergie que transporte une onde sonore par unité de temps à travers une surface donnée. Elle dépend de l'amplitude de cette onde sonore et de la surface.

Dans le cas général, elle est donnée par la formule :

${\displaystyle {\mathcal {P}}=\iint \limits _{S}\mathrm {I} \,\mathrm {d} S}$

où P est la puissance, I est l'intensité sonore, et dS l'élément de surface atteint par l'onde sonore.

Pour une source isolée, le calcul de la puissance acoustique totale émise correspond à l'intégrale ci-dessus étendue sur une surface fermée.

En France, le domaine de l'automobile, l'administration et les assureurs utilisent une puissance dite « fiscale » pour déterminer le montant de certaines taxes et primes. Cette puissance est dimensionnée en « cheval fiscal » (noté « CV » en droit fiscal français), qui n'est en rien comparable à une puissance au sens physique. Depuis juillet 1998, la puissance fiscale dépend de la valeur normalisée d'émission de dioxyde de carbone (CO₂) en g/km et de la puissance maximale du moteur en kW. Si on note C la quantité de CO₂ rejetée (en g/km) et P la puissance du moteur (en kW) la puissance fiscale est : ${\displaystyle P_{CV}={\frac {C}{45}}+\left({\frac {P}{40}}\right)^{1{,}6}}$ ;

En Belgique, seule la cylindrée du moteur est prise en compte pour le calcul de la puissance fiscale^[4],[5].

• Vecteur de Poynting, en électromagnétisme, pour la puissance instantanée.
• Ordres de grandeur de puissance

• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Den Store Danske Encyklopædi
  • Store norske leksikon
• Notices d'autorité :

  • LCCN
  • GND
  • Israël
  • Tchéquie
• Exemple d'outil permettant le calcul de puissance d'un moteur électrique pour le transfert de charges à plat et sur plan incliné

• Portail de la physique
• Portail de l’énergie
• Portail du génie mécanique
• Portail de l’électricité et de l’électronique