Équations de Jefimenko
En électromagnétisme, les équations de Jefimenko, nommées d'après Oleg D. Jefimenko , donnent le champ électrique et le champ magnétique dus à une distribution de charges électriques et de courant électrique dans l'espace. Elles prennent en compte le retard dû à la propagation des champs (temps « retardé ») en raison de la valeur finie de la vitesse de la lumière et des effets relativistes. Elles peuvent donc être utilisées pour des charges et des courants en déplacement. Elles sont les solutions générales des équations de Maxwell pour n'importe quelle distribution arbitraire de charges et de courants[1],[2].
Les équations
Les champs électrique et magnétique
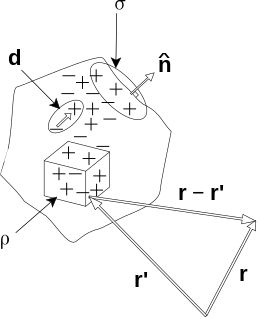

Les équations de Jefimenko donnent le champ E et le champ B produits par une charge arbitraire ou une distribution de courant, de densité de charge ρ et de densité de courant J[3] :
où r' est un point dans la distribution de charge, r est un point dans l'espace, et
est le temps retardé . Il y a des expressions similaires pour D et H[4].
Ces équations sont la généralisation, dépendant du temps (électrodynamique), de la loi de Coulomb et de la loi de Biot et Savart, qui étaient à l'origine vraies uniquement pour les champs en électrostatique et en magnétostatique ainsi que pour les courants continus.
Les potentiels retardés comme origine
Les équations de Jefimenko peuvent être déduites[5] à partir des potentiels retardé φ et A :
qui sont les solutions des équations de Maxwell formulées sous forme des potentiels en remplaçant φ et A dans les équations de E et B en fonction des potentiels (potentiels électromagnétiques) :
Enfin en utilisant la relation :
on trouve les champs E et B en fonction des sources, c'est-à-dire les densités de charge ρ et les densités de courant J et non plus en fonction des potentiels φ et A.
Discussion
Une interprétation largement répandue des équations de Maxwell dit que des champs électriques et magnétiques variables s'engendrent l'un l'autre dans l'espace et donc donnent naissance à des ondes électromagnétiques qui se propagent[6] (onde électromagnétique). Néanmoins, les équations de Jefimenko suggèrent une autre explication[7]. Jefimenko disait : « […] ni les équations de Maxwell, ni leurs solutions, ne montrent l'existence de lien causal entre le champ électrique et magnétique. En conséquence, l'on doit conclure que le champ électromagnétique est une entité mixte qui possède toujours une composante électrique et magnétique créées simultanément par leurs sources communes à savoir des charges et des courants électriques variables »[8].
McDonald dit[9] que les équations de Jefimenko semblent être apparues pour la première fois en 1962 dans la seconde édition du livre « Classical Electricity and Magnetism » de Panofsky et Phillips[10]. Cependant David Griffiths clarifie cela comme ceci : « la première apparition explicite de ces équations dont j'ai connaissance est due à Oleg Jefimenko en 1966 » et il considère les équations du livre de Panofsky et Phillips comme seulement « fort proches »[11].
Les caractéristiques essentielles des équations de Jefimenko se voient dans leurs seconds membres où apparaît le temps « retardé » ce qui reflète la « causalité » de ces équations. En d'autre termes, les premiers membres des équations sont en réalité causés par les seconds membres, contrairement aux équations différentielles de Maxwell où les deux membres fonctionnent simultanément. Dans les équations de Maxwell il n'y a aucun doute que les deux membres de chaque équation sont égaux, mais comme Jefimenko l'indique : « […] comme chacune de ces équations relie des quantités simultanées dans le temps, aucune ne peut représenter une relation causale »[12]. Une autre caractéristique des équations de Jefimenko est que l'expression de E ne dépend pas de B et vice-versa. En conséquence il est impossible que les champs E et B se créent l'un l'autre. Ce sont les densités de charge et les courants électriques qui les créent.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jefimenko's equations » (voir la liste des auteurs).
- ↑ Jefimenko 1989.
- ↑ (en) David J. Griffiths et Mark A. Heald, « Time-dependent generalizations of the Biot–Savart and Coulomb laws », American Journal of Physics, no 59 (2), , p. 111-117 (lire en ligne, consulté le ).
- ↑ Introduction to Electrodynamics (3rd Edition), D. J. Griffiths, Pearson Education, Dorling Kindersley, 2007, (ISBN 81-7758-293-3).
- ↑ Oleg D. Jefimenko, Solutions of Maxwell's equations for electric and magnetic fields in arbitrary media, American Journal of Physics 60 (10) (1992), 899–902.
- ↑ Introduction to Electrodynamics (3rd Edition), D. J. Griffiths, Pearson Education, Dorling Kindersley, 2007, (ISBN 81-7758-293-3)
- ↑ Paul Kinsler, « How to be causal: time, spacetime, and spectra », Eur. J. Phys., vol. 32, , p. 1687 (DOI 10.1088/0143-0807/32/6/022, Bibcode 2011EJPh...32.1687K, arXiv 1106.1792)
- ↑ Jefimenko 2000, p. 16 (chap. 1, sec. 1-4).
- ↑ Jefimenko 2000, p. 16 (chap. 1, sec. 1-5).
- ↑ Kirk T. McDonald, The relation between expressions for time-dependent electromagnetic fields given by Jefimenko and by Panofsky and Phillips, American Journal of Physics 65 (11) (1997), 1074-1076.
- ↑ Wolfgang K. H. Panofsky, Melba Phillips, Classical Electricity And Magnetism, Addison-Wesley (2nd. ed - 1962), Section 14.3. The electric field is written in a slightly different - but completely equivalent - form. Reprint: Dover Publications (2005), (ISBN 978-0-486-43924-2).
- ↑ David J. Griffiths, Introduction to Electrodynamics, Prentice Hall (New Jersey), 3rd edition (1999), pp. 427—429
- ↑ Jefimenko 2000, p. 6 (chap. 1, sec. 1-1).
Bibliographie
- (en) Oleg D. Jefimenko, Electricity and Magnetism : An Introduction to the Theory of Electric and Magnetic Fields, New-York, Appleton-Century-Crofts, , 1re éd.
- (en) Oleg D. Jefimenko, Electricity and Magnetism : An Introduction to the Theory of Electric and Magnetic Fields, Star City, Electret Scientific, , 2e éd., 597 p. (ISBN 978-0-917406-08-9).
- (en) Oleg D. Jefimenko, Causality Electromagnetic Induction and Gravitation, Star City, Electret Scientific, , 2e éd., 210 p. (ISBN 0-917406-23-0).

![{\displaystyle \mathbf {E} (\mathbf {r} ,t)={\frac {1}{4\pi \epsilon _{0}}}\int \left[\left({\frac {\rho (\mathbf {r} ',t_{r})}{|\mathbf {r} -\mathbf {r} '|^{3}}}+{\frac {1}{|\mathbf {r} -\mathbf {r} '|^{2}c}}{\frac {\partial \rho (\mathbf {r} ',t_{r})}{\partial t}}\right)(\mathbf {r} -\mathbf {r} ')-{\frac {1}{|\mathbf {r} -\mathbf {r} '|c^{2}}}{\frac {\partial \mathbf {J} (\mathbf {r} ',t_{r})}{\partial t}}\right]dV',}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a90b95ca17cd00ed7495d2e4c60d14d2485c1c)
![{\displaystyle \mathbf {B} (\mathbf {r} ,t)={\frac {\mu _{0}}{4\pi }}\int \left[{\frac {\mathbf {J} (\mathbf {r} ',t_{r})}{|\mathbf {r} -\mathbf {r} '|^{3}}}+{\frac {1}{|\mathbf {r} -\mathbf {r} '|^{2}c}}{\frac {\partial \mathbf {J} (\mathbf {r} ',t_{r})}{\partial t}}\right]\times (\mathbf {r} -\mathbf {r} ')\,dV',}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5973b1ac40894eea4e24a3e2789ab4035ade141f)



