Densité de courant
| Unités SI | A m−2 |
|---|---|
| Dimension | I L−2 |
| Nature | Grandeur vectorielle intensive |
| Symbole usuel | |
| Lien à d'autres grandeurs |
|
La densité de courant, ou densité volumique de courant, est un vecteur qui décrit le courant électrique à l'échelle locale, en tout point d'un système physique. Dans le Système international d'unités, son module s'exprime en ampères par mètre carré (A/m2 ou A m−2). À l'échelle du système tout entier il s'agit d'un champ de vecteurs, puisque le vecteur densité de courant est défini en tout point.
Quand l'électricité circule essentiellement à la surface d'un objet (notamment celle d'un conducteur parcouru par un courant électrique de haute fréquence), on définit la densité surfacique de courant, également vectorielle, dont le module s'exprime en ampères par mètre (A/m ou A m−1).
Quand l'électricité circule dans un conducteur filiforme (de dimensions latérales très petites en comparaison de sa longueur), on définit la densité linéique de courant, un vecteur parallèle au fil, dirigé dans le sens du courant et dont le module est l'intensité électrique, exprimée en ampères (A).
Définition
Densité volumique
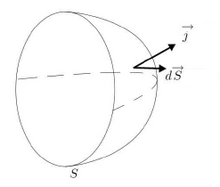
Un courant électrique est un débit de charges électriques à travers une surface orientée. Pour une surface élémentaire décrite par son vecteur normal , l'intensité du courant traversant cette surface et , le vecteur densité de courant en ce point, sont reliés par :
- .
Pour obtenir l'intensité du courant à travers une surface finie S, on intègre cette relation sur la surface totale :
- .
Le signe de I est alors lié à l'orientation de la surface S.
Densité surfacique
Une densité de courant est par défaut une densité de courant volumique. Si l'on considère un conducteur dont une des dimensions est très faible devant les deux autres (une plaque d'épaisseur e), on peut définir la densité surfacique de courant :
où z désigne une coordonnée mesurée perpendiculairement à la surface.
L'intensité du courant passant à travers une ligne tracée sur la surface est alors
où la ligne est décrite par son vecteur normal .
Densité linéique
On peut de même définir la densité linéique de courant, pour les circuits électriques classiques (où les conducteurs sont des fils de section faible par rapport à leur longueur) :
où l'intégrale est étendue à l'ensemble d'une section S du fil.
L'intensité électrique circulant dans le fil est alors :
- .
En d'autres termes, la densité linéique est le vecteur :
- , où est un vecteur unitaire tangent au fil et dirigé dans le sens du courant.
Lien avec la densité de flux
Le courant électrique pouvant être considéré comme un débit de charges, le vecteur densité de courant est directement proportionnel à la somme des vecteurs densités de flux des différentes espèces chargées qui participent au courant[1] :
avec
- la vitesse moyenne de l'espèce numérotée i au point considéré;
- la densité volumique de l'espèce numérotée i au point considéré;
- la charge électrique de l'espèce numérotée i.
La somme s'étend à toutes les espèces chargées présentes. Par suite de ces définitions, le vecteur
- est le vecteur densité de flux d'une espèce.
Lien avec l'équation de Maxwell-Ampère
Dans le domaine de l'électromagnétisme, les équations de Maxwell permettent de décrire la propagation d'une onde électromagnétique. La 4e équation (appelée équation de Maxwell-Ampère) fait intervenir la densité de courant circulant au sein du matériau traversé par l'onde électromagnétique étudiée.
On part de l'équation de Maxwell-Ampère :
où est le champ magnétique, la perméabilité du vide et la densité de courant totale, s'exprimant :
- .
Dans cette expression, on peut détailler :
- la densité de courant de conduction (on reconnaît la loi d'Ohm locale) , avec σ la conductivité,
- la densité de courant de polarisation , où est le vecteur de polarisation,
- la densité de courant d'aimantation , où est le vecteur aimantation,
- la densité de courant de déplacement , où est la permittivité du vide.
Applications
Électromagnétisme et électrotechnique
La densité de courant est utilisée pour manipuler les phénomènes de conduction électrique à l'échelle locale, notamment dans :
- la loi d'Ohm locale ;
- l'effet Joule local ;
- l'expression de la conservation de la charge électrique ;
- l'équation de Maxwell-Ampère ;
- les définitions de la conductivité et de la résistivité.
Géophysique
Les électromètres à densité de courant sont utilisés dans le domaine de la géophysique marine pour appréhender les valeurs de conductivité électrique du sous–sol [2],[3],[4].
Physiologie humaine
Le courant induit dans l’organisme humain est généralement exprimé en densité de courant (produit du champ électrique interne et de la conductivité du corps humain). Par exemple, en cas d'exposition à des champs électromagnétiques d'extrêmement basse fréquence (50 Hz typiquement) « l’hypothèse simplificatrice d’une conductivité homogène du corps humain de 0,2 siemens par mètre est utilisée »[5].
Défaillance due à une densité de courant excessive
Une densité de courant trop élevée peut être une cause de défaillance pour un dispositif :
- pour un fil électrique, une surchauffe, avec des conséquences telles qu’un incendie ou la fusion du conducteur[6],[7] ;
- pour un supraconducteur, la perte de supraconductivité par dépassement de la densité de courant critique[8],[9] ;
- pour un circuit intégré, où les densités de courant peuvent être très élevées, la défaillance par électromigration[10] (cf. équation de Black)[11].
Notes et références
- ↑ (en) Keith W. Whites, « Magnetostatics », dans Wai-Kai Chen, The Electrical Engineering Handbook, Elsevier Academic Press, (ISBN 0-12-170960-4), p. 480.
- ↑ Stéphane Sainson, Electrographies de fond de mer. Une révolution dans la prospection pétrolière, Cachan. Ed. Lavoisier 2012
- ↑ Stéphane Sainson, La prospection électromagnétique du pétrole sous-marin, Industrie et Technologies n°962, février 2014
- ↑ Jean-François Préveraud, Forer jusqu'à la dernière goutte, Industrie et Technologies n°964, avril 2014
- ↑ Direction générale de la santé (France)(2014) Champs électromagnétiques d’extrêmement basse fréquence - Effets sur la santé (DGS février 2014)
- ↑ Gérald Huguenin, « Cours de technologie électrique et électronique : courant électrique », sur HE-Arc, (consulté le )
- ↑ La défaillance par fusion est l'effet recherché dans le cas d'un fusible, afin de protéger l'installation électrique.
- ↑ Pascal Tixador et Yves Brunet, « Supraconducteurs - Structure et comportement des fils », Conversion de l'énergie électrique, (DOI 10.51257/a-v1-d2702, lire en ligne, consulté le )
- ↑ Abdelaziz Ramzi, Etude de l'aimantation irréversible, de la densité de courant critique et de la susceptibilité dans les nouveaux supraconducteurs (thèse de doctorat), Agadir, Faculté des Sciences d'Agadir, (lire en ligne)
- ↑ Simon Gousseau, Caractérisation in operando de l’endommagement par électromigration des interconnexions 3D : Vers un modèle éléments finis prédictif (thèse de doctorat en sciences et génie des matériaux), Sophia Antipolis, Mines ParisTech - CEMEF, (lire en ligne)
- ↑ J. R. Black, Mass Transport of Aluminum by Momentum Exchange with Conducting Electrons, 6th Reliability Physics Symposium, 1967

































