Verre de spin
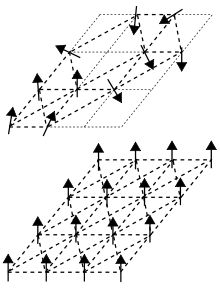

Les verres de spin sont des alliages métalliques comportant un petit nombre d'impuretés magnétiques disposées au hasard dans l'alliage. À chaque impureté est associée un spin. Le couplage entre ces différents spins peut être plus ou moins intense - attractif ou répulsif - en fonction de la distance qui les sépare. Les physiciens les modélisent statistiquement par des spins d'Ising (plus ou moins un) couplés par des constantes aléatoires représentant le désordre. Ces constantes n'évoluent que lentement à mesure que le verre de spin vieillit et que les impuretés diffusent, c'est pourquoi ces couplages sont dits gelés, ou indépendant du temps (quenched). Souvent, on considère que ces couplages suivent une distribution gaussienne.
En physique théorique, parler des verres de spin revient à parler de ces modèles (cf ci-dessous). Mais il existe de nombreuses réalisations expérimentales de ces systèmes. Les verres de spin constituent le paradigme des systèmes désordonnés, qui, avec la physique des processus hors équilibre, constituent une grande part des travaux de ce domaine dans les dernières années. Les verres de spin sont dits frustrés : selon des chemins différents, deux spins se donnent des instructions contradictoires. Les modèles les plus connus sont ceux d'Edwards-Anderson [1]où l'on ne considère que les couplages entre plus proches voisins sur un réseau hypercubique, et de Sherington et Kirpatrick[2], où toutes les paires de spins interagissent entre elles (graphe complet), et qui est censé tenir compte des interactions à grande distance. Ces modèles se résument donc à se donner un hamiltonien, ainsi qu'une distribution de probabilité (le plus souvent gaussienne avec une valeur moyenne nulle, ce qui donne une probabilité égale aux interactions ferromagnétiques et antiferromagnétiques) pour les couplages.
Étymologie
Pourquoi les verres de spin sont-ils appelés verres ? Un verre est un état de la matière à mi-chemin entre le liquide et le solide et qui possède un grand nombre d'états métastables de basse énergie. Quand le verre refroidit, il est généralement bloqué, non pas dans l'état fondamental, mais dans un de ces états métastables de basse énergie. Il en va de même des verres de spins qui possèdent un paysage composé de beaucoup d'états métastables dans les basses énergies. Il met un très grand temps pour franchir les différentes barrières et rejoindre finalement l'état fondamental (vieillissement). C'est pourquoi les constantes de couplages sont considérées comme gelées relativement aux configurations de spin (variables dynamiques), et qu'il y a lieu de considérer deux échelles de temps.
Propriétés
Les états purs de basse énergie présentent des propriétés d'ultramétricité. Leur répartition est ultramétrique.
Les difficultés rencontrées pour calculer l'énergie libre des verres de spin a donné naissance à la méthode des répliques[1] et à la notion de brisure de symétrie des répliques. Une autre approche utilisant le champ de réaction d'Onsager est due à Thouless, Anderson et Palmer[3].
Les applications des verres de spin sont nombreuses : depuis les problèmes d'optimisation (économie, etc.) jusqu'en biologie (modélisation des neurones, apprentissages).
Les verres de spin nous donnent un exemple de phénomènes de « vieillissement » qui sont aussi caractéristiques des verres structuraux, polymériques, diélectriques, et des colloïdes. Ils présentent des effets de rajeunissement sous l’effet de l’application d’un champ magnétique assez fort, comme les verres peuvent être rajeunis par l’application d’une contrainte. Mais les verres de spin montrent aussi des effets non-triviaux de rajeunissement et mémoire en fonction de la température, effets que certaines études récentes montrent pouvoir aussi exister, quoique moins marqués, dans certains polymères et gels.
Les réalisations pratiques des verres de spin consistent en des matériaux faits d’atomes magnétiques entre lesquels les interactions sont aléatoirement ferro- ou antiferro-magnétiques. La situation la plus connue est celle d’alliages inter-métalliques, obtenus par la dilution de quelques pourcents d’atomes magnétiques dans une matrice métallique non-magnétique ; d’autres verres de spin, aux propriétés strictement équivalentes, sont obtenus par dilution de composés magnétiques isolants. Dans ces systèmes, les moments magnétiques ne peuvent satisfaire simultanément les interactions magnétiques contradictoires auxquelles ils sont soumis par leurs voisins. Cette frustration conduit à l’existence d’une multitude d’états métastables, séparés par des barrières d’énergie de toutes tailles, qui dominent le comportement magnétique des verres de spin en produisant des temps de réponse à toutes les échelles à partir du microscopique (~ s), sans limite supérieure observée. Les verres de spin se présentent à nous comme perpétuellement hors d’équilibre.
La dynamique lente des verres de spin montre d’intéressantes analogies avec celle des verres structuraux ou polymériques. Une procédure expérimentale standard d’étude de ces propriétés consiste à refroidir le verre de spin jusqu’en dessous de sa température de gel Tg (typiquement vers 0,5 à 0,9 Tg) en présence d’un faible champ magnétique H, à attendre pendant un temps tw (l’aimantation reste à très peu près constante), pour ensuite couper ce champ à t=0 et mesurer la relaxation vers zéro de l’aimantation, dite |« thermo-rémanente » (TRM). Cette relaxation s’étend sur plusieurs décades de temps, et de plus dépend du temps d’attente tw : plus tw est grand, plus la relaxation est lente, le verre de spin « durcit ».
Ce phénomène de vieillissement est exactement semblable à celui observé dans la relaxation du module élastique des polymères vitreux. Il obéit d’ailleurs aux mêmes lois d’échelles ; les courbes correspondant à deux valeurs tw1 et tw2 sont à peu près espacées de μ.log tw1/ tw2, avec μ≤1. Ceci suggère une loi d’échelle en t/twμ ; plus exactement, on utilise λ/twμ, où λ est un temps effectif rendant compte de l’effet du vieillissement au cours de la relaxation elle-même (à temps courts λ~t). Cette variable réduite permet de superposer avec une grande précision les relaxations mesurées pour des tw variant sur de larges gammes. L’exposant μ mesuré dans les verres de spin reste toujours inférieur à 1, même dans la limite des champs très faibles. Il diminue lorsque l’amplitude du champ magnétique H (dont la coupure provoque la relaxation) augmente[4]. Il existe des effets dits de « rajeunissement et mémoire »[évasif][5]
Notes et références
- S F Edwards et P W Anderson, « Theory of spin glasses. II », Journal of Physics F: Metal Physics, vol. 6, no 10, , p. 1927–1937 (ISSN 0305-4608, DOI 10.1088/0305-4608/6/10/022, lire en ligne, consulté le )
- ↑ (en) David Sherrington et Scott Kirkpatrick, « Solvable model of a spin-glass », Physics Review Letters, vol. 35, no 26, , p. 1792-1796 (DOI 10.1103/PhysRevLett.35.1792)
- ↑ (en) D. J. Thouless, P. W. Anderson et R. G. Palmer, « Solution of 'Solvable model of a spin glass' », Philosophical Magazine, vol. 35, no 3, , p. 593–601 (ISSN 0031-8086, DOI 10.1080/14786437708235992, lire en ligne, consulté le )
- ↑ Dupuis et al., Phénomènes de vieillissement, rajeunissement et mémoire : l’exemple des verres de spin, arXiv:cond-mat/0205628
- ↑ E. Vincent, Aging, rejuvenation and memory : the example of spin glasses, arXiv:cond-mat/0603583
Voir aussi
Bibliographie
- (en) Spin glass theory and beyond de Parisi, Mézard etc.
- (en) Viktor Dotsenko, An Introduction to the theory of spin glasses and neural networks, World Scientific, 1994
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :
- [ps] Verres de spin et optimisation combinatoire : notes de séminaire de M. Talagrand présentant quelques résultats et enjeux sur les verres de spin, 1999.

