Théorie quantique des champs

La théorie quantique des champs est une approche en physique théorique pour construire des modèles décrivant l'évolution des particules, en particulier leur apparition ou disparition lors des processus d'interaction. Il ne s'agit donc pas d'une seule théorie, mais plutôt d'un cadre théorique, qui tire son nom de la combinaison entre la notion classique de champ et des principes et outils de la mécanique quantique relativiste. Selon cette approche, l'attention est portée non pas sur des particules, mais sur des champs, pénétrant l'espace et considérés comme plus fondamentaux.

Développée au cours du XX^e siècle, surtout entre 1920 et 1950 par des physiciens tels que Dirac, Fock, Pauli, Tomonaga, Schwinger, Feynman et Dyson, la théorie quantique des champs est aujourd'hui un des piliers conceptuels de la description physique de l'univers, au travers notamment du modèle standard. À ce titre le développement de la théorie a été récompensé par de nombreux prix Nobel de physique, et les progrès mathématiques nécessaires pour lui donner corps ont donné lieu à plusieurs médailles Fields.

Toutefois, en dépit de nombreux efforts, il ne semble pas possible d'y intégrer une description de la théorie de la relativité générale. Pour cette raison, de nombreux physiciens cherchent une théorie plus générale, dont la théorie quantique des champs (et la théorie de la relativité générale) ne seraient que des approximations.

La théorie quantique des champs a été développée initialement pour comprendre les phénomènes de physique des hautes énergies au sein des accélérateurs de particules, ce pour quoi elle est principalement utilisée aujourd'hui. Mais elle permet également d'expliquer des phénomènes de physique de la matière condensée, tels que la supraconductivité, l'effet Hall quantique, ou la superfluidité.

Crédit image:

Auteur inconnuUnknown author

licence CC BY-SA 3.0 de 🛈

Le développement de la mécanique quantique, à la fin du XIX^e siècle et au début du XX^e siècle, se concentrait sur la notion de « particule », héritée de la physique classique. Les premiers travaux de Dirac, Heisenberg et Schrödinger culminent ainsi dans une description nouvelle des propriétés des particules élémentaires, capables d'expliquer avec succès les observations expérimentales, par exemple dans la prédiction des spectres d'émission atomiques. Ce succès sur les systèmes isolés constitués de particules en nombre restreint et prescrit, laissait toutefois de côté de nombreuses questions, notamment en ce qui concerne l'interaction entre matière et rayonnement.

Par ailleurs, plusieurs tentatives de concilier l'équation de Schrödinger avec la mécanique relativiste avaient été suivies, donnant notamment naissance à l'équation de Klein-Gordon et à l'équation de Dirac, l'une et l'autre soulevant des difficultés théoriques et d'interprétation. Par analogie avec le champ électromagnétique, décrit par les équations de Maxwell, il est possible d'associer à chacune de ces équations un champ, et une densité de lagrangien d'où l'équation découle par le principe de moindre action.

Champ	Équation	Densité de lagrangien
Scalaire ${\displaystyle \phi \ }$ (Spin = 0)	${\displaystyle 0=(\square +m^{2})\phi }$	${\displaystyle {\mathcal {L}}=(\partial _{\mu }\phi ^{\dagger })(\partial ^{\,\mu }\phi )-m^{2}\phi ^{\dagger }\phi }$
Spineur ${\displaystyle \psi \ }$ (Spin = 1/2)	${\displaystyle 0=(i\gamma ^{\mu }\partial _{\mu }-m)\psi }$	${\displaystyle {\mathcal {L}}={\tfrac {i}{2}}\left({\overline {\psi }}\gamma ^{\mu }(\partial _{\mu }\psi )-(\partial _{\mu }{\overline {\psi }})\gamma ^{\mu }\psi \right)-m{\overline {\psi }}\psi }$
Photon ${\displaystyle A^{\mu }\ }$ (Spin 1)	${\displaystyle 0=\partial _{\mu }F^{\mu \nu }=\square A^{\nu }-\partial ^{\nu }(\partial _{\mu }A^{\mu })}$	${\displaystyle {\mathcal {L}}=-{\tfrac {1}{4}}F_{\mu \nu }F^{\mu \nu }=-{\tfrac {1}{2}}(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })}$

Néanmoins il s'agit encore de champs n'interagissant pas entre eux, et le nombre de particules est fixé. Impossible donc de décrire la création ni l'absorption de ces particules avec ce formalisme.

S'appuyant sur des intuitions mises en avant par Born, Jordan et Heisenberg^[1], c'est Dirac qui proposera le premier une théorie quantique du rayonnement en 1927^[2]. S'intéressant d'abord au rayonnement électromagnétique, Dirac propose une procédure de passage à la limite, et s'appuie sur le modèle de l'oscillateur harmonique quantique pour expliquer l'apparition et l'absorption de photons.

Poursuivant cet effort, Jordan introduit les opérateurs de création et d'annihilation et la notion de « seconde quantification ». Après des difficultés initiales pour garantir la cohérence de la théorie (notamment l'invariance relativiste), une première théorie quantique des champs électromagnétique est ainsi proposée dès 1929 par Werner Heisenberg et Wolfgang Pauli^[3],[4].

Le succès rapide des méthodes de théorie quantique des champs, par exemple dans le calcul de la diffusion Compton, n'occultait pas certains problèmes. D'une part, il existait un écart non négligeable entre les prédictions et les mesures dans plusieurs expériences impliquant les rayons cosmiques. D'autre part, et plus inquiétant pour la cohérence de la théorie, le développement des calculs au-delà du premier ordre, par des méthodes perturbatives, donnait lieu à des séries divergentes. Ainsi par exemple, la self énergie de l'électron, ou les fluctuations du champ électromagnétique, étaient « infinis » selon la théorie.

Plusieurs formes de divergences infinie apparaissent ainsi dans l'application directe des méthodes de la théorie quantique des champs. Des tentatives naïves (de troncation, de soustraction des termes divergents, etc.) pour gérer les infinis n'ont abouti qu'à des approches mathématiquement contradictoires, des résultats éloignés des expériences, ou des violations des lois de conservation physique.

En dépit de ces doutes sur la solidité de la théorie, ces méthodes sont appliquées en 1933 par Fermi au problème de la radioactivité β, pour décrire l'interaction faible. Puis, en 1934, Pauli et Weisskopf appliquent les techniques de théorie quantique des champs à l'équation de Klein-Gordon, et montrent qu'elle décrit l'évolution d'un champ scalaire. Néanmoins, ces progrès étaient tous suspendus par les doutes qui pesaient sur l'avenir de la théorie.

Crédit image:

• Freeman_Dyson.jpg: Taken by Flickr user ioerror, Jacob Appelbaum

Original téléversé par Jamesmorrison sur Wikipédia anglais.

• derivative work: Sven Manguard

licence CC BY-SA 3.0 🛈

Il fallut attendre la fin de la Seconde Guerre mondiale pour que soit proposée une méthode cohérente et systématique pour gérer les divergences : la technique de renormalisation. C'est en 1949 que cette technique naît avec un article de Freeman Dyson^[5], dans lequel il réconcilie des propositions de la génération de physiciens qui l'a précédé : Hans Bethe^[6], Julian Schwinger^{[7],[8],[9],[10]}, Richard Feynman^{[11],[12],[13]} et Shin'ichiro Tomonaga^{[14],[15],[16],[17],[18],[19],[20]}.

En 1955, Lehmann, Symanzik et Zimmerman montrent comment obtenir, à partir d'une densité de lagrangien, les observables physiques de la matrice de diffusion : c'est la formule de réduction LSZ ^[21], qui va grandement faciliter le travail des théoriciens et des expérimentateurs, en traduisant les propriétés des théories quantiques en prédictions expérimentales.

D'un côté, la renormalisation résout les difficultés effectives en faisant disparaître les infinis des résultats : ainsi, le calcul du moment magnétique anomal de l'électron et du décalage de Lamb atteignent un niveau de précision inégalé précédemment. De l'autre côté, la conséquence de cette approche est que certaines grandeurs, comme la charge et la masse de l'électron, ne peuvent pas être déduites de la théorie et doivent donc être fixées « de l'extérieur ». La théorie quantique des champs électromagnétiques, ou électrodynamique quantique, ne peut donc pas prétendre au statut de théorie fondamentale car il demeure à expliquer les valeurs de ces paramètres.

Le succès expérimental de l'électrodynamique quantique, et les résultats préliminaires de Fermi sur l'interaction faible, motivèrent la recherche d'autres phénomènes que la théorie quantique des champs pourrait expliquer. Une théorie se développe pour l'interaction forte, et un lien est établi par Murray Gell-Mann entre les groupes de symétries et les théories quantiques des champs : c'est la notion de théorie de jauge. En associant les descriptions quantiques de l'électromagnétisme, de l'interaction faible et de l'interaction forte, on obtient une théorie renormalisable associée au groupe SU(3) × SU(2) × U(1), appelée « modèle standard ».

Cette théorie (qui est bien plus qu'un modèle) a été développée par Sheldon Glashow, Steven Weinberg et Abdus Salam entre 1959 et 1967, qui montrent notamment que l'interaction faible et l'interaction électromagnétique sont issues d'une même interaction, dite électrofaible. Puis par Frank Wilczek, David Gross et David Politzer qui expliquent en 1973 le comportement de l'interaction forte, introduisant la notion de liberté asymptotique. Enfin, les travaux de Peter Higgs, François Englert, Robert Brout permettent de comprendre le mécanisme par lequel certaines interactions, qui selon la théorie devraient avoir une portée infinie, ont en fait une portée très limitée : il s'agit d'un couplage à un champ scalaire, le boson de Higgs-Englert-Brout.

Ce champ scalaire apparaît du fait d'un mécanisme de brisure spontanée de symétrie, dont Martin Veltman et Gerard 't Hooft ont montré qu'il était renormalisable en 1971.

Crédit image:

Betsy Devine

licence CC BY-SA 3.0 🛈

Le modèle standard permet de prédire l'existence de particules : six types de leptons et six types de quarks, chacune de ces 12 particules étant un fermion de spin 1/2 ; chaque interaction est associée à des particules de spin 1 : le photon pour l'interaction électromagnétique, les bosons W et Z pour l'interaction faible, les gluons pour l'interaction forte. Toutes les particules prédites par la théorie ont été mesurées expérimentalement ; le boson de Higgs, le dernier à avoir été confirmé, a été mesuré pour la première fois en 2011 au LHC.

Malgré les succès impressionnants des théories quantiques des champs, plusieurs questions et problèmes ont été soulevés, qui constituent aujourd'hui des axes de recherche encore ouverts.

D'une part la théorie s'est construite par ajouts successifs de mécanismes et d'outils, et il est naturel de chercher une description mathématique cohérente de cet ensemble. Les axiomes de Wightman, proposés en 1956, cherchent à contraindre toute théorie des champs visant à décrire la nature ; des jeux d'axiomes alternatifs ont été proposés, par Haag-Araki en 1962, par Haag-Kastler, ou par Osterwalder-Schrader notamment.

L'intérêt d'une base axiomatique est la possibilité de démontrer formellement des résultats qui seraient autrement des observations expérimentales difficiles à expliquer, comme le théorème spin-statistique ou le théorème CPT, et qui sont promus au rang de résultats généraux s'appliquant à toute théorie quantique des champs.

Au cours des années 1980, le point de vue a changé, avec la découverte notamment des phénomènes tels que l'effet Hall quantique, dans lequel il n'y a pas de brisure spontanée de symétrie. Pour un tel système, c'est la topologie et non la géométrie qui est responsable de la physique observée. Dans le cas de l'effet Hall, une théorie des champs effective basée sur la théorie de Chern-Simons a pu être construite : la question fut alors posée de développer, pour les théories du modèle standard, si une telle extension était possible.

D'un côté, cela a engendré tout un corps de recherche associé à Michael Atiyah, Graeme Segal, Edward Witten, Richard Borcherds et Maxim Kontsevich qui cherchent à construire une théorie topologique des champs quantiques (TQFT). D'un autre côté, le développement de théories invariantes d'échelle, dites théories conformes, ont montré comment saisir de nombreux phénomènes physiques tels que les transitions de phase, et au travers de la correspondance AdS/CFT dessinent un lien entre théories quantiques et cosmologie.

Enfin, les paramètres des théories (dont le modèle standard) sont encore mal compris, et il n'existe pas à l'heure actuelle de mécanisme permettant de quantifier sans incohérences des théories comme la relativité générale ; associées à des difficultés mathématiques, comme le problème ouvert du gap de masse des théories de Yang-Mills, ces questions poussent à la recherche de nouvelles approches ou de meilleurs outils.

La théorie quantique telle qu'initialement développée décrivait un ensemble de particules au moyen d'une fonction d'onde ${\displaystyle \psi (r_{1},\dotsc ,r_{n},t)}$, qui permet de calculer la probabilité de mesurer une particule en un point donné de l'espace. Une telle fonction évolue dans le temps selon l'équation de Schrödinger : ${\displaystyle {\hat {H}}\psi ={\hat {E}}\psi }$, où ${\displaystyle {\hat {H}}}$ est l'opérateur hamiltonien et ${\displaystyle {\hat {E}}}$ est l'opérateur énergie.

Néanmoins, ce formalisme ne permet pas de capturer plusieurs phénomènes physiques, notamment :

• La création ou la disparition de particules, qui est observée expérimentalement dans les accélérateurs lors de collisions à hautes énergies, ou lors des processus de désintégration^[22].
• Les effets de la relativité, l'équation de Schrödinger étant définie dans le référentiel du laboratoire et n'étant donc pas invariante de Lorentz. Ici encore, ces effets sont manifestes dans les accélérateurs de particules, mais également dans l'étude des rayonnements cosmiques, qui pénètrent l'atmosphère terrestre à des vitesses proches de celles de la lumière^[23].
• Les interactions avec les champs générés par les particules elles-mêmes posent des difficultés, et il n'est pas possible de décrire d'un seul tenant les particules et les champs qu'elles génèrent, par exemple s'il s'agit d'électrons en mouvement^[24].

Les tentatives de corriger l'invariance relativiste de l'équation de Schrödinger, qui ont donné lieu aux équations de Klein-Gordon, puis de Dirac, se heurtent en fait à une incohérence structurelle : une théorie relativiste de particules en interaction ne peut pas supposer un nombre constant de particules.

La théorie classique de l'électromagnétisme, décrite par les équations de Maxwell, est relativiste. On peut déduire l'évolution d'un champ électromagnétique via le principe de moindre action, c'est-à-dire que le champ effectivement observé physiquement rend minimal la quantité$${\displaystyle {\displaystyle {\mathcal {S}}[\phi ]=\int {{\mathcal {L}}(\mathbf {x} ,\phi ,\partial _{\mu }\phi )\ \mathrm {d} ^{4}x}.}}$$appelée action, et calculée à partir du lagrangien associé au champ. Les méthodes variationnelles classiques donnent alors les équations de champ comme une solution aux équations d'Euler-Lagrange :$${\displaystyle {\displaystyle {\frac {\delta {\mathcal {S}}}{\delta \phi }}={\frac {\partial {\mathcal {L}}}{\partial \phi }}-\partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\phi )}}\right)=0}}$$

Ainsi, l'évolution du champ magnétique est déterminée par sa densité de lagrangien : $${\displaystyle {\mathcal {L}}=-{\tfrac {1}{4}}F_{\mu \nu }F^{\mu \nu }=-{\tfrac {1}{2}}(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }).}$$

La théorie quantique des champs prend le même point de départ : une densité de lagrangien est fixée pour le champ d'intérêt. Cependant, au lieu de déterminer les équations d'évolution par le principe de moindre action, qui est un principe classique, un procédé de quantification est appliqué.

La quantification canonique (historiquement appelée seconde quantification), est une procédure permettant d'obtenir une théorie quantique à partir d'une théorie classique, en s'efforçant de conserver la structure de la théorie, notamment ses symétries, autant que possible. Le nom de seconde quantification vient de ce que la théorie quantique développée auparavant traitait les particules dans un cadre quantique, mais les champs (au travers de l'énergie potentielle) étaient encore classiques. Cette approche partielle, qualifiée de première quantification, laisse donc la place à un traitement intégralement quantique des phénomènes physiques.

La procédure de quantification canonique suit le principe suivant, dû initialement à Dirac : on associe au champ ${\displaystyle \phi }$ le moment canonique ${\displaystyle \pi }$ via une transformée de Legendre, puis ${\displaystyle \phi }$ et ${\displaystyle \pi }$ sont promus au rang d'opérateurs et dotés des relations de commutation canoniques :$${\displaystyle [\phi (x),\phi (y)]=0\qquad \ [\pi (x),\pi (y)]=0\qquad [\phi (x),\pi (y)]=i\hbar \delta (x-y).}$$

Illustrons ce mécanisme sur le champ libre classique, de densité lagrangienne$${\displaystyle {\mathcal {L}}(\phi )={\frac {1}{2}}(\partial _{t}\phi )^{2}-{\frac {1}{2}}(\partial _{x}\phi )^{2}-{\frac {1}{2}}m^{2}\phi ^{2}}$$En travaillant dans le domaine de Fourier,$${\displaystyle \phi _{k}=\int \phi (x)e^{-ikx}\,\mathrm {d} x,\ \ \pi _{k}=\int \pi (x)e^{-ikx}\,\mathrm {d} x}$$et puisque les champs sont à valeurs réelles, ${\displaystyle \phi _{-k}=\phi _{k}^{\dagger }}$ et ${\displaystyle \pi _{-k}=\pi _{k}^{\dagger }}$. Le hamiltonien classique associé au champ ${\displaystyle \phi }$ s'écrit$${\displaystyle H={\frac {1}{2}}\sum _{k=-\infty }^{\infty }\left[\pi _{k}\pi _{k}^{\dagger }+\omega _{k}^{2}\phi _{k}\phi _{k}^{\dagger }\right]}$$où on a posé ${\displaystyle \omega _{k}={\sqrt {k^{2}+m^{2}}}}$. Autrement dit, il s'agit d'une collection d'oscillateurs harmoniques indépendants. La quantification, via l'utilisation des relations de commutation canonique, donne alors le hamiltonien comme une collection d'oscillateurs quantiques, et les opérateurs d'échelle $${\displaystyle a_{k}={\frac {1}{\sqrt {2\hbar \omega _{k}}}}\left(\omega _{k}\phi _{k}+i\pi _{k}\right),\ \ a_{k}^{\dagger }={\frac {1}{\sqrt {2\hbar \omega _{k}}}}\left(\omega _{k}\phi _{k}^{\dagger }-i\pi _{k}^{\dagger }\right)}$$permettent d'écrire l'opérateur hamiltonien ainsi :$${\displaystyle H=\sum _{k=-\infty }^{\infty }\hbar \omega _{k}a_{k}^{\dagger }a_{k}}$$Dans ce contexte, les opérateurs d'échelle s'interprètent donc comme la création ou la destruction d'une particule, et l'état de plus basse énergie est assimilé au vide. Pour des champs en interaction, la notion de vide peut être plus complexe, entre autres parce que des effets de polarisation apparaissent.

La densité de lagrangien associée au champ libre en tant que théorie quantique est alors $${\displaystyle {{\mathcal {L}}_{\mathrm {libre} }}=(\partial _{\mu }\phi ^{\dagger })(\partial ^{\mu }\phi )-m^{2}\phi ^{\dagger }\phi .}$$

Une approche alternative pour obtenir une théorie quantique des champs est la méthode des intégrales de chemin. Elle repose sur une reformulation du principe de moindre action, où ce n'est plus la trajectoire qui minimise l'action, car cette notion n'a plus de sens en mécanique quantique. À la place, on considère une somme pondérée sur toutes les trajectoires possibles, qui prend la forme d'une intégrale :$${\displaystyle Z\propto \int [\mathrm {d} \phi ]\exp \left[iS(\phi )\right]}$$ici, ${\displaystyle \int [\mathrm {d} \phi ]}$ désigne une intégrale prise sur toutes les configurations de champ possible. En pratique, cette quantité est calculée par un processus de limite, le champ étant découpé sur une grille de plus en plus fine. L'utilisation de propagateurs permet alors de calculer les propriétés recherchées, comme les probabilités de transition.

Parmi les intérêts de cette approche, elle rend visible l'invariance de Lorentz dans les équations, car les coordonnées de temps et d'espace y jouent un rôle très clairement identique, ce qui n'est pas du tout clair dans la formulation de la quantification canonique. L'utilisation du formalisme lagrangien, plutôt que hamiltonien, laisse également au physicien une intuition parfois plus claire. En revanche, d'autres propriétés sont moins évidentes, comme la conservation de la probabilité.

Quoi qu'il en soit, on sait aujourd'hui que les deux approches, quantification canonique et intégrales de chemin, sont équivalentes.

La quantification canonique du champ libre donne un hamiltonien qui correspond à une collection d'oscillateurs harmoniques, dont l'énergie totale est conservée : il s'agit de la somme des énergies individuelles de chaque particule. Ces particules n'interagissent pas, et évoluent librement ; leur nombre est conservé car aucun processus d'interaction ne vient les détruire ni en ajouter. Cette conservation n'est pas imposée a priori, comme c'était le cas avec l'approche quantique à base de fonction d'onde : il s'agit d'un résultat des équations de champ obtenues.

Ainsi ce champ peut être décrit en termes de nombre d'occupation, c'est-à-dire la donnée, pour chaque niveau d'énergie, du nombre de particules qui occupent ce niveau. Ces particules sont indiscernables : elles n'interviennent dans la théorie qu'au travers de leur niveau d'énergie ; par exemple, échanger deux particules n'a aucun effet physique et ne constitue donc pas un état différent. Par ailleurs, il n'y a pas de contrainte sur le nombre de particules qui peuvent occuper un niveau d'énergie : le principe d'exclusion de Pauli ne s'applique pas, et le champ libre héberge donc des bosons.

Il est possible d'obtenir un champ libre de fermions : lors du processus de quantification, ce sont des règles d'anti-commutation qui sont imposées (ou, par la méthode des intégrales de chemin, l'utilisation de variables grassmanniennes).

Un des résultats que permet de montrer la théorie des champs est le théorème spin-statistique, qui dit ceci : les particules de spin entier sont des bosons, et les particules de spin demi-entier sont les fermions. Formulé d'abord en 1939 par Markus Fierz et Wolfgang Pauli^[25],[26], ce principe a d'abord été vérifié sur les théories de champs libres, mais ils ne pouvaient pas le démontrer en général. Une première preuve générale est donnée par Julian Schwinger en 1950^[27], et depuis plusieurs dizaines de preuves ont été établies^[28] qui cherchent entre autres à satisfaire le souhait de Feynman qu'un principe aussi facile à énoncer puisse être aisé à expliquer^[29].

Les interactions entre particules sont la conséquence de non linéarités dans le champ quantifié, sous la forme par exemple de produits du champ dans le lagrangien ou dans le hamiltonien. La quasi-totalité des théories d'intérêt en physique sont des théories avec des interactions. Par exemple :

• L'interaction de Yukawa, qui se manifeste entre les nucléons dans un noyau atomique, est décrite par l'interaction entre un champ décrivant le nucléon, noté ${\displaystyle \psi }$, et un champ décrivant le méson ${\displaystyle \pi }$ noté ${\displaystyle \phi }$. Cette interaction est capturée par un terme proportionnel à ${\displaystyle \phi {\bar {\psi }}\psi }$.
• Le champ de Higgs, associé au boson H, est décrit par un champ ${\displaystyle \Phi }$ qui interagit avec lui-même, selon un terme proportionnel à ${\displaystyle \Phi ^{4}}$en première approximation (voir ci-dessous « théorie φ⁴ »).
• L'interaction électromagnétique, associée au photon, agit sur les particules chargées selon un terme proportionnel à ${\displaystyle A_{\mu }{\bar {\psi }}\gamma ^{\mu }\psi }$.

On associe à ces produits une constante numérique, appelée constante de couplage, qui mesure l'intensité relative de l'interaction. En général, il n'est pas possible de calculer exactement les solutions pour un champ en interaction. Plutôt, des approximations successives sont obtenues en tronquant un développement en séries où les puissances des constantes de couplage apparaissent : c'est l'approche perturbative. Cette méthode fonctionne bien pour l'interaction électromagnétique, car la constante de couplage électromagnétique aux basses énergies est petite, ${\displaystyle \alpha \approx 1/137}$, et les puissances de ce nombre tendent rapidement vers 0. Ce n'est pas le cas des autres interactions, et il n'est pas en général possible de traiter les champs en interaction complètement par le seul moyen d'une approche perturbative.

Dans une expérience de collision, des particules sont préparées dans un état initial, puis accélérées afin de subir des collisions à hautes énergies. Les produits de la collision sont alors mesurés. Une des grandeurs importantes est donc la probabilité de mesurer un certain état final, étant donné un certain état initial. On peut ramener cette question au calcul d'une matrice S (matrice de diffusion ou de « scattering »), qui donne alors la probabilité recherchée au travers de l'amplitude ${\displaystyle \langle \psi _{\mathrm {initial} }|S|\psi _{\mathrm {final} }\rangle }$.

Cette matrice ${\displaystyle S}$ n'est en général pas connue, mais peut être exprimée comme un développement perturbatif du hamiltonien d'interaction au travers de la série de Dyson, ou plus prosaïquement : $${\displaystyle S=1-ig{\hat {H}}_{\text{int}}-g^{2}{\hat {H}}_{\text{int}}^{2}+\ldots }$$où ${\displaystyle g}$ est la constante de couplage, supposée faible.

Le physicien américain Richard Feynman a proposé en 1948 un ensemble de règles permettant d'effectuer ce calcul de probabilités au travers de diagrammes, qui portent aujourd'hui son nom. Suivant la philosophie de l'intégrale de chemin, et conservant un caractère intuitif, la démarche consiste à établir pour un processus donné tous les scénarios possibles ayant le même état initial et le même état final. Tous ces scénarios ne sont pas aussi probables les uns que les autres, ils sont donc pondérés en conséquence. Négliger les scénarios les moins probables revient à tronquer le développement perturbatif à un certain ordre. Ainsi, le processus de diffusion Compton, dans lequel un électron et un photon interagissent, se décompose en plusieurs diagrammes :

Crédit image:

• ElectronPositronAnnihilation.svg: Dirk Hünniger, Joel Holdsworth
• derivative work: kismalac

licence CC BY-SA 3.0 🛈

Dans chaque diagramme, l'électron est représenté par une ligne pleine fléchée, et le photon par une ligne ondulée. Les particules créées et absorbées au cours de l'interaction, qui n'apparaissent pas dans l'état final, sont dites virtuelles. Elles ne sont pas mesurables dans le laboratoire, mais contribuent au calcul de la probabilité totale.

L'ordre du diagramme correspond au nombre de nœuds, ainsi dans l'illustration ci-dessus les deux premiers diagrammes sont d'ordre 2, et le troisième diagramme est d'ordre 4. Les diagrammes d'ordre supérieur contribuent des corrections de plus en plus petites à la probabilité recherchée, lorsque la constante de couplage est assez faible.

Les diagrammes de Feynman constituent ainsi un outil privilégié en théorie quantique des champs^{[30],[31],[32]}. Toutefois, ils ne sont utilisables que dans les contextes où un développement perturbatif est possible, ce qui n'est pas le cas pour l'étude du confinement en QCD par exemple, ni pour le traitement de solutions localisées comme les solitons ou les instantons de certaines théories.

L'approche perturbative possède en fait des limites même dans le régime où les interactions sont faibles. Dans le développement en diagrammes de Feynman du processus de diffusion Compton ci-dessus, le troisième diagramme est en fait divergent^[33].

La technique de renormalisation a été développée pour éliminer ces divergences, ne laissant derrière que des quantités finies et physiquement mesurables. L'idée clé est que les divergences proviennent d'une extrapolation à des échelles arbitrairement petites (ou, ce qui revient au même, à des échelles d'énergies arbitrairement grandes). Par exemple, le diagramme divergent en question fait apparaître la self énergie de l'électron, en tant que sous-diagramme :

Ici l'électron émet un photon, qui est immédiatement réabsorbé. Il faut ajouter toutes les contributions provenant des positions et moments que peuvent prendre ces particules dans ce scénario, ce qui donne une self énergie$${\displaystyle \Sigma =e_{0}^{2}\int \mathrm {d} ^{4}k{\frac {k_{\mu }\gamma ^{\mu }+m_{0}}{(k^{2}+m_{0}^{2})(k-p)^{2}}}\sim \int _{0}^{\infty }\mathrm {d} |k|\,{\frac {|k|^{4}}{|k|^{4}}}}$$Or cette expression est divergente. Cet infini est non physique^{[Note 1]}, et peut être évité par l'approche suivante (dont l'intuition se retrouve chez Stueckelberg et Bethe) formalisée par Schwinger, et systématisée par Feynman, Dyson, et Tomonaga : elle consiste à redéfinir la masse et la charge de l'électron qui interviennent dans cette équation, ${\displaystyle e_{0}}$ et ${\displaystyle m_{0}}$. On obtient une théorie régularisée, qui n'est plus aussi précise, mais qui ne possède plus de divergences. Les valeurs de ${\displaystyle e_{0}}$ et ${\displaystyle m_{0}}$ utilisées, qui ne correspondent pas à ce qui est mesuré sur les particules, sont dites « nues » : les inévitables interactions avec le champ alentour modifiant la quantité mesurée. Seules les valeurs nues sont fondamentales, et les quantités définies en termes de ces valeurs ne divergent pas^[34].

Cette manière d'éliminer les divergences, appelée renormalisation, donne en pratique d'excellents résultats. Mais plus fondamentalement, elle informe sur la nature des divergences dans les théories quantiques des champs. Il arrive qu'il ne soit pas possible d'absorber ainsi dans les paramètres de la théorie les phénomènes de divergence. On distingue ainsi les théories des champs « renormalisables » de celles qui ne le sont pas. En particulier, les théories du modèle standard sont renormalisables, mais ce n'est pas le cas de la théorie de la relativité générale par exemple.

Dans la théorie classique de l'électromagnétisme, le potentiel vecteur jouit d'une propriété remarquable appelée invariance de jauge. Concrètement, on peut ajouter le gradient d'une fonction arbitraire au potentiel vecteur, cela n'a aucun effet sur les équations d'évolution des champs et donc sur la physique. Cette invariance s'interprète comme une symétrie locale de la théorie, qui doit être prise en compte de même que les symétries globales lors de la quantification. Pour l'électromagnétisme, ou sa version quantifiée l'électrodynamique quantique, cette symétrie correspond au groupe ${\displaystyle U(1)}$ qui est commutatif et de rang 1, dit groupe de jauge de l'électromagnétisme.

La symétrie est capturée lors de la quantification par la présence d'un champ de jauge, dont les particules correspondent aux générateurs du groupe de jauge : dans le cas de l'électromagnétisme, ${\displaystyle U(1)}$ est engendré par un seul élément, qui correspond au photon. Une théorie de jauge est ainsi une théorie quantique des champs dans laquelle l'interaction est portée par les particules d'un champ de jauge, dont on peut montrer qu'elles sont des bosons.

Dans le cas général, le groupe de jauge n'est pas nécessairement commutatif, c'est notamment le cas des théories de Yang-Mills. Le boson de jauge dans le cas non commutatif porte lui-même une charge (contrairement au cas commutatif, où le photon par exemple est neutre). Les couleurs^{[Note 2]} de particules correspondent à la représentation fondamentale du groupe, et les bosons de jauge à la représentation adjointe. Ainsi pour le groupe ${\displaystyle SU(3)}$, il y a trois couleurs de particules (les quarks) et 8 couleurs de bosons de jauge (les gluons), ces derniers correspondant aux matrices de Gell-Mann.

Le modèle standard est une théorie de jauge, pour le groupe de symétrie ${\displaystyle U(1)\times SU(2)\times SU(3)}$, et d'une manière générique les théories de jauges ont de bonnes propriétés mathématiques et physiques. La théorie de la relativité générale peut aussi être formulée comme une théorie de jauge, associée à la conservation de l'énergie et de l'impulsion ; il ne s'agit toutefois pas d'une théorie renormalisable.

Crédit image:

Gonis

licence CC BY-SA 3.0 🛈

Crédit image:

Cjean42

licence CC BY-SA 3.0 🛈

L'existence de symétries exactes pour les théories de jauge garantit que les bosons de jauge sont sans masse. Or l'expérience montre que l'interaction faible et forte sont de portée limitée, de l'ordre du femtomètre, ce qui semble en contradiction avec une masse nulle. De même, les fermions qui composent la matière^{[Note 3]} devraient posséder une masse nulle, une prédiction également en violent contraste avec l'expérience.

La solution fut trouvée par le concours de trois groupes indépendants de chercheurs dans les années 1960 : Robert Brout et François Englert; Peter Higgs; et Gerald Guralnik, C. R. Hagen et Tom Kibble. Il s'agit du mécanisme de Brout-Englert-Higgs-Hagen-Guralnik-Kibble, qui a valu à Brout et Englert le prix Nobel de physique en 2013, un an après que le CERN a annoncé la découverte expérimentale du boson de Higgs prédit par ce mécanisme.

L'idée clé est d'expliquer l'acquisition de la masse des bosons de jauge comme un phénomène de brisure spontanée de symétrie, s'étant produit avec le refroidissement de l'Univers. Dans ce scénario, un champ dit de Higgs initialement compatible avec les symétries de jauge et couplé aux bosons présente progressivement une instabilité centrale en « chapeau mexicain » : de manière analogue au flambage d'une poutre sous la pression, des conditions symétriques donnent lieu à une solution asymétrique de plus basse énergie. Cette asymétrie se manifeste mathématiquement comme un terme quadratique analogue à un terme de masse, et en ce sens la brisure de symétrie dote les bosons de jauge d'une masse non nulle.

S'agissant d'un phénomène géométrique, tous les bosons ne sont pas affectés identiquement. Par exemple, le modèle standard décrit aujourd'hui l'interaction électromagnétique (dont les bosons de jauge, les photons, sont sans masse) et l'interaction faible (dont les bosons sont massifs) comme le résultat d'une brisure spontanée de symétrie sur une interaction électrofaible dont tous les bosons sont sans masse. L'unification électrofaible a valu à Sheldon Glashow, Abdus Salam et Steven Weinberg le prix Nobel de physique en 1979.

Le mécanisme exact de brisure de symétrie dans le cas électrofaible peut être décrit en analysant le lagrangien correspondant, mais il est souvent plus pratique de travailler sur un modèle simplifié, comme la théorie φ⁴ décrite plus bas, pour développer les outils et l'intuition physique du phénomène.

Notons enfin que le mécanisme de brisure de symétrie n'apporte pas de réponse quant aux grandes différences de masse observées parmi les particules élémentaires, notamment entre le quark le plus léger et le plus lourd, et ne donne pas de borne inférieure sur les masses pouvant apparaître dans la théorie. La preuve de l'existence d'un gap de masse dans les théories des champs quantiques constitue l'un des problèmes du prix du millénaire.

Trois symétries discrètes jouent un rôle particulier dans les théories quantiques des champs. Il s'agit de la symétrie de renversement du temps, notée T ; de la symétrie de renversement de l'espace, notée P ; et de la symétrie de renversement des charges, notée C. Un théorème, initialement démontré par Schwinger en 1951 (puis développé et raffiné par Lüders, Pauli, Bell et d'autres) montre qu'une application simultanée des trois symétries C, P et T laisse toutes les observables invariantes : autrement dit, il n'est pas possible de distinguer notre univers d'un univers identique auquel on aurait appliqué une symétrie CPT. Ce résultat fondamental porte le nom de théorème CPT (ou parfois théorème de Lüders-Pauli) et repose sur des hypothèses minimales d'invariance de Lorentz et de localité^{[Note 4]}.

On pourrait croire qu'il en est de même pour une symétrie prise indépendamment, par exemple P. Cependant, des expériences des années 1950 sur l'interaction faible (notamment l'expérience de Wu sur la désintégration bêta du cobalt 60) montrent que la symétrie P est violée. De même, l'application d'une symétrie C uniquement aurait pu laisser les lois de la physique invariantes, mais une telle symétrie transforme par exemple un neutrino de chiralité gauche en un antineutrino de chiralité gauche, or ce dernier n'interagit pas dans le modèle standard. Ainsi C est également violée.

Enfin, la symétrie composée CP est également violée^{[Note 5]}, un résultat découvert en 1964 et qui a valu à James Watson Cronin and Val Fitch le prix Nobel de physique 1980. Leur expérience s'appuie sur l'existence des kaons neutres, qui peuvent se transformer en leur propre antiparticule (chaque quark devenant l'anti-quark de l'autre), mais avec une probabilité différente dans un sens et dans l'autre. Ces violations de la symétrie CP ont depuis été confirmées, par exemple dans les expériences NA31, NA48 du CERN, ou KTev du Fermilab, et d'autres violations de CP ont été obtenues sur les mésons B dans les expériences BaBar et Belle au début des années 2000. Mathématiquement, l'existence de la violation CP est capturée par les matrices de mélange (matrice CKM et PMNS) ; à l'heure actuelle aucune théorie n'explique les valeurs mesurées expérimentalement pour ces matrices.

De manière intéressante, expérimentalement, aucune violation de CP n'est observée pour les processus dépendants de l'interaction forte (décrite en théorie des champs par la chromodynamique quantique). Rien n'interdit pourtant une telle violation dans le lagrangien de QCD, et l'absence de violation apparaît en fait comme un ajustement particulièrement heureux de paramètres : on parle du « problème CP de l'interaction forte ». Le modèle standard n'explique pas ce phénomène, qui constitue l'une des motivations (et une des contraintes) pour les théories alternatives.

Peu après la découverte du neutron, dont la masse est sensiblement similaire à celle du proton, Heisenberg a proposé un modèle dans lequel proton et neutron sont deux états d'une même particule, ce qui donnerait un mécanisme par lequel un proton se transforme en neutron ou vice versa. Par analogie avec le spin électronique, Wigner a introduit le terme de spin isotopique, ou « isospin » pour décrire cette théorie.

Avec la découverte au cours du XX^e siècle de nombreux hadrons et mésons, l'idée de les regrouper par masse et de les traiter comme des multiplets d'isospin a été un des principes classificateurs qui a finalement abouti à la théorie des quarks. L'isospin est une symétrie de l'interaction forte sous l'action de SU(2), dont le traitement mathématique est analogue à celui du spin électronique et se généralise bien à des multiplets plus larges, et peut être adaptée à d'autres contextes (comme l'isospin faible pour les bosons W).

On sait cependant que la masse du neutron diffère de celle du proton (ce qui correspond à une différence de masse entre les quarks up et down, et aux effets de l'interaction électromagnétique) ; par ailleurs les quarks s, c, b, t découverts depuis ont des masses encore très différentes. Il n'est donc pas possible d'étendre l'isospin à tous les quarks, car une théorie SU(6) fournirait des prédictions qualitativement et quantitativement incorrectes.

Néanmoins, les symétries approchées restent des outils utiles pour simplifier ou comprendre une théorie des champs.

La supersymétrie est une symétrie supposée entre fermions et bosons. Elle associe à chaque particule d'un type une particule partenaire de l'autre type.

Comme l'isospin, il s'agit d'abord d'un principe classificateur, qui permettrait de regrouper la compréhension de plusieurs phénomènes ; une première version de la supersymétrie fut proposée par Miyazawa en 1966, entre mésons et baryons. Cependant le théorème de Coleman-Mandula interdit l'introduction de nouvelles symétries scalaires au groupe de Poincaré.

Néanmoins autour de 1971 différents physiciens saisissent et corrigent l'idée (Gervais-Sakita en 1971, Golfand-Likhtman en 1971, Volkov-Akulov en 1972, Wess et Zumino en 1974), ce qui permit notamment d'en dégager la structure mathématique. En 1975, le théorème de Haag-Łopuszański-Sohnius légitime ces efforts et montre qu'il est possible dans une certaine mesure de contourner le théorème de Coleman-Mandula, au prix de remplacer l'algèbre de Lie des symétries par une superalgèbre de Lie, les nouvelles symétries correspondant à l'ajout de spineurs. C'est une justification a posteriori de la cohérence de la théorie de Wess-Zumino, la première théorie supersymétrique renormalisable.

En 1977, Fayet propose une extension minimale du modèle standard pour y incorporer la supersymétrie, et prédit l'existence de nombreuses particules super-partenaires. Même si aucune des particules super-partenaires supposées n'ont aujourd'hui été observées dans les expériences de collisionneur, l'élégance théorique de la supersymétrie en fait un candidat sérieux et un outil efficace, qui motive également des travaux mathématiques (l'étude des superalgèbres de Lie gradées).

Les modèles supersymétriques sont contraints par l'expérience à basse énergie : la mesure du moment magnétique anomal du muon (Fermilab), la densité de matière noire (WMAP), les détecteurs directs (XENON-100 et LUX). Ils sont également contraints par les expériences de collision au LHC, Tevatron et au LEPC. Les expériences UA1 et UA2 effectuées au SPS du CERN ont posé des limites sur les masses des squarks et des gluinos (partenaires supersymétriques des quarks et gluons respectivement), plus tard renforcées par le LEP, puis par l'expérience D0 du Tevatron en 2006. Les résultats de WMAP montrent qu'une théorie supersymétrique doit inclure un mécanisme réduisant fortement la densité de neutralinos (le partenaire du neutrino) sans quoi ils ne peuvent expliquer la densité de matière noire observée.

Les expériences du LHC, qui ont permis la découverte du boson de Higgs en 2011-2012 à 125 GeV, ont également confirmé un couplage aux fermions et au boson cohérents avec le modèle standard, sans trace de superpartenaires^[35]. La théorie MSSM peine à expliquer l'absence de détections de superpartenaires à une telle énergie, qui nécessite pour s'accommoder de l'expérience d'importantes corrections radiatives des squarks stop (de l'ordre du TeV). Ces corrections n'étant pas motivées théoriquement, le pouvoir explicatif de cette théorie particulière s'en voit fortement diminué. Des expériences sont en cours pour contraindre davantage les théories supersymétriques, telles que XENON-1T.

En l'absence d'interactions, on obtient une théorie quantique du champ libre, correspondant au lagrangien de Klein-Gordon avec source :

$${\displaystyle {\mathcal {L}}_{\textrm {libre}}=J\phi -{\frac {1}{2}}\partial ^{\mu }\phi \partial _{\mu }\phi -{\frac {1}{2}}m^{2}\phi ^{2}}$$

Dans cette équation, ${\displaystyle J}$ est un terme source d'origine externe, et ${\displaystyle m}$ est la masse de la particule considérée. Pour obtenir les grandeurs d'intérêt physique, on porte attention à l'amplitude de diffusion, obtenue via la formule de réduction LSZ :

$${\displaystyle Z_{0}=\langle 0|0\rangle =\int {\mathcal {D}}\phi \,\exp \left(i\int \mathrm {d} ^{4}x\,{\mathcal {L}}\right)}$$où l'état ${\displaystyle |0\rangle }$est le vide de la théorie. Pour évaluer cette amplitude, qui dépend a priori de ${\displaystyle J}$, on considère les transformées de Fourier ${\displaystyle {\hat {\phi }}}$et ${\displaystyle {\hat {J}}}$de ${\displaystyle \phi }$et ${\displaystyle J}$respectivement, et on pose ${\displaystyle {\hat {\varphi }}(k)={\hat {\phi }}(k)-{\frac {{\hat {J}}(k)}{k^{2}+m^{2}}}}$, ce qui permet d'écrire$${\displaystyle \int \mathrm {d} ^{4}x\,{\mathcal {L}}={\frac {1}{2}}\int {\frac {\mathrm {d} ^{4}k}{(2\pi )^{4}}}\left({\frac {{\hat {J}}(k){\hat {J}}(-k)}{k^{2}+m^{2}}}-{\hat {\varphi }}(k)(k^{2}+m^{2}){\hat {\varphi }}(-k)\right)}$$Puisque ${\displaystyle {\mathcal {D}}\phi ={\mathcal {D}}\varphi }$on obtient alors ${\displaystyle Z_{0}(J=0)=0}$et

$${\displaystyle Z_{0}(J)=\exp \left({\frac {i}{2}}\int \mathrm {d} ^{4}x\,\mathrm {d} ^{4}y\,J(x)\Delta (x-y)J(y)\right)}$$

où ${\displaystyle \Delta }$est le propagateur de Feynman, qui est une fonction de Green pour l'équation de Klein-Gordon. On obtient ainsi, par exemple, que ${\displaystyle \langle 0|\mathrm {T} \phi (x)\phi (y)|0\rangle =-i\Delta (y-x)}$, qui est un cas particulier du théorème de Wick. Sans surprise, dans une théorie de champ libre, les particules se propagent indépendamment les unes des autres. Ainsi, on connaît toutes les solutions exactes de la théorie : l'espace de Hilbert est l'espace de Fock des états à plusieurs particules créés à partir du vide ${\displaystyle |0\rangle }$.

La plus simple théorie quantique décrivant des champs neutres (scalaires) en interaction fait apparaître un terme d'ordre 4, c'est la « théorie φ⁴ ». Si elle n'est pas motivée par une réalité physique, cette théorie simple présente déjà de nombreux phénomènes intéressants (dont une brisure spontanée de symétrie) et peut servir de modèle approché pour comprendre les interactions plus complexes des théories physiques. Des solutions exactes à cette théorie sont connues^[36]. Le choix de l'exposant 4 s'explique d'une part par la volonté d'avoir un champ d'interactions (il faut donc un exposant plus grand que 2) et d'autre part par le mauvais comportement de l'exposant 3, qui donne lieu à des solutions non bornées et présente un point critique instable à l'origine^[37]. La théorie φ⁴ est donc bien en ce sens la plus simple.

La densité de lagrangien de la théorie est celle d'une particule libre, ajoutée d'un terme d'auto-interaction quadratique :$${\displaystyle {\mathcal {L}}_{\phi ^{4}}=(\partial _{\mu }\phi ^{\dagger })(\partial ^{\mu }\phi )-m^{2}\phi ^{\dagger }\phi -{\frac {\lambda }{4}}(\phi ^{\dagger }\phi )^{2}}$$Les règles de Feynman correspondant à ce lagrangien sont illustrées dans la figure ci-dessous :

Crédit image:

Pra1998

licence CC BY-SA 4.0 🛈

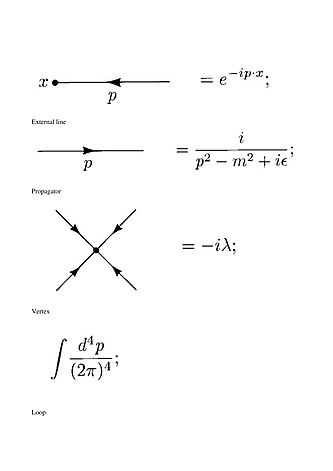
Lorsque m² devient négative mais que λ reste positif, le vide dégénère : une brisure de symétrie apparaît, et avec elle des états collectifs intéressants. En vertu du théorème de Goldstone, cette brisure donne notamment naissance à un boson. En particulier, c'est une des manières de comprendre le mécanisme de Brout-Englert-Higgs.

L'électrodynamique quantique est une théorie de jauge abélienne pour le groupe U(1), déterminée par la densité de lagrangien :$${\displaystyle {\begin{aligned}{{\mathcal {L}}_{\textrm {QED}}}={}&{\bar {\psi }}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }\\={}&i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma _{\mu }(A^{\mu }+B^{\mu })\psi -m{\bar {\psi }}\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }\end{aligned}}}$$Dans cette équation, ${\displaystyle \gamma ^{\mu }}$correspond aux matrices de Dirac, le champ ${\displaystyle \psi }$ décrit l'évolution des particules (électrons et positrons), ${\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}}$est l'adjoint de Dirac du champ,${\displaystyle D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }\,\!}$ est la dérivée covariante de jauge, e est la constante de couplage de la théorie autrement dit la charge électrique de la particule correspondante, m est la masse de l'électron et du positron, ${\displaystyle A_{\mu }}$est le 4-potentiel électromagnétique covariant engendré par l'électron, ${\displaystyle B_{\mu }}$est un éventuel champ externe, et enfin${\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\,\!}$est le tenseur électromagnétique. La charge et la masse des particules (électrons et positrons) est sujette à renormalisation.

La théorie de l'électrodynamique quantique est certainement la théorie quantique des champs « réaliste » la mieux comprise, et la faible valeur de la constante de couplage permet l'introduction de méthodes perturbatives très efficaces, en accord impressionnant avec l'expérience^[38]. On sait en revanche que la théorie n'est qu'une approximation : d'une part elle est mal définie aux hautes énergies^[39],[40] ; d'autre part l'interaction électromagnétique est indissociable de l'interaction faible, et il faut donc aborder les deux phénomènes de manière conjointe sous l'angle de la théorie électrofaible.

La théorie de l'interaction électrofaible a pour densité de lagrangien :$${\displaystyle {\begin{aligned}{\mathcal {L}}_{\textrm {EW}}={}&-{\frac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\frac {1}{4}}B^{\mu \nu }B_{\mu \nu }\\&+{\overline {Q}}_{i}iD\!\!\!\!/\;Q_{i}+{\overline {u}}_{i}^{c}iD\!\!\!\!/\;u_{i}^{c}+{\overline {d}}_{i}^{c}iD\!\!\!\!/\;d_{i}^{c}+{\overline {L}}_{i}iD\!\!\!\!/\;L_{i}+{\overline {e}}_{i}^{c}iD\!\!\!\!/\;e_{i}^{c}\\&+|D_{\mu }h|^{2}-\lambda \left(|h|^{2}-{\frac {v^{2}}{2}}\right)^{2}\\&-y_{u\,ij}\epsilon ^{ab}\,h_{b}^{\dagger }\,{\overline {Q}}_{ia}u_{j}^{c}-y_{d\,ij}\,h\,{\overline {Q}}_{i}d_{j}^{c}-y_{e\,ij}\,h\,{\overline {L}}_{i}e_{j}^{c}+hc\end{aligned}}}$$Les termes correspondent aux phénomènes suivants :

• La première ligne décrit l'interaction entre les trois bosons W et le boson B. Les bosons W₁, W₂, W₃ engendrent le groupe SU(2) d'isospin faible, tandis que le boson B engendre le groupe U(1) d'hypercharge faible.
• La deuxième ligne, qui fait intervenir des dérivées covariantes et la notation slash de Feynman, couple les bosons de jauge aux fermions.
• La troisième ligne correspond au champ de Higgs électrofaible. La valeur dans ${\displaystyle h=0}$est instable, ce qui est responsable d'une brisure de symétrie qui fixe ${\displaystyle |h|=v/4}$ avec une phase arbitraire.
• La quatrième ligne correspond à l'interaction de Yukawa ; après brisure du champ de Higgs, ce terme sera responsable de la masse des fermions.

Après brisure de symétrie, qui se produit autour de 246 GeV, le champ de Higgs acquiert une valeur moyenne non nulle dans le vide. On peut alors réécrire le lagrangien en faisant explicitement apparaître le champ de Higgs. Le couplage résiduel au champ de Higgs s'interprète alors comme des termes de masse pour les bosons de jauge (et pour le boson de Higgs).

De plus, les champs subissent un mélange, responsable de l'apparition du photon γ et du boson Z d'une part, et de bosons W^± d'autre part :

${\displaystyle {\begin{pmatrix}\gamma \\Z^{0}\end{pmatrix}}={\begin{pmatrix}\cos \theta _{W}&\sin \theta _{W}\\-\sin \theta _{W}&\cos \theta _{W}\end{pmatrix}}{\begin{pmatrix}B\\W_{3}\end{pmatrix}}}$

${\displaystyle {\displaystyle W^{\pm }={\frac {1}{\sqrt {2}}}(W_{1}\mp iW_{2}).}}$

L'angle θ_W est appelé angle de Weinberg. Sa valeur n'est pas prédite par le modèle standard, et il n'y a pas aujourd'hui de théorie faisant consensus pour déterminer la valeur de l'angle de Weinberg. Cependant, des expériences précises contraignent les valeurs possibles. Le CODATA donne en 2014 la valeur

${\displaystyle \sin ^{2}\theta _{\text{W}}=1-(m_{\text{W}}/m_{\text{Z}})^{2}=0.2223(21)}$

correspondant à un angle θ_W autour de 30 degrés.

La chromodynamique quantique est une théorie de jauge pour SU(3), décrite par la densité de lagrangien :$${\displaystyle {\mathcal {L}}_{\mathrm {QCD} }(q,A)={\bar {q}}\left(i\gamma ^{\mu }D_{\mu }-m\right)q-{\frac {1}{4}}F_{\mu \nu }^{a}F_{a}^{\mu \nu }}$$Dans cette expression ${\displaystyle q}$ est le champ de quarks, ${\displaystyle D_{\mu }}$ est la dérivée covariante de jauge, ${\displaystyle \gamma ^{\mu }}$ sont les matrices de Dirac, et ${\displaystyle F_{\mu \nu }^{a}}$ est le tenseur chromodynamique. Ce dernier est analogue au tenseur électromagnétique en QED, si ce n'est qu'il correspond à trois couleurs au lieu de deux charges. Le tenseur chromodynamique s'écrit explicitement$${\displaystyle F_{\mu \nu }^{a}=\partial _{\mu }{\mathcal {A}}_{\nu }^{a}-\partial _{\nu }{\mathcal {A}}_{\mu }^{a}+gf^{abc}{\mathcal {A}}_{\mu }^{b}{\mathcal {A}}_{\nu }^{c}}$$ où ${\displaystyle {\mathcal {A}}_{\mu }^{a}(x)}$ correspond aux champs de gluons de couleur ${\displaystyle a}$ et ${\displaystyle f^{abc}}$ sont les constantes de structure de SU(3).

Le lagrangien fait également apparaître la masse ${\displaystyle m}$des quarks et la constante de couplage ${\displaystyle g}$, ces deux quantités étant sujettes à la renormalisation.

Ainsi la QCD décrit deux champs : quarks et gluons, et leurs interactions. Les quarks sont des fermions massifs de spin 1/2 portant une charge de couleur et une charge électrique (-1/3 ou +2/3). Les gluons sont des bosons sans masse de spin 1, neutres électriquement, qui portent également une charge de couleur.

La motivation initiale, et la principale application, du développement des théories quantiques des champs est d'expliquer et prédire les résultats des expériences à haute énergie, telles qu'observées dans les collisionneurs et accélérateurs de particules. Le modèle standard, assemblé à partir des théories quantiques de jauge pour trois des quatre interactions fondamentales (la gravité ne se prêtant pas à ce formalisme), est en accord remarquable avec l'expérience et a permis la prédiction de nombreuses particules. Toutes les particules prédites par le modèle standard ont été observées, les deux dernières étant le quark top (prédit en 1973, observé en 1995, prix Nobel 2008) et le boson de Higgs (prédit en 1964, observé en 2011, prix Nobel 2013).

L'électrodynamique quantique (QED) peut être traitée dans une large mesure par des méthodes perturbatives, mais pour l'instant les solutions exactes sont confinées à des situations très restrictives (en dimension 2 par exemple). La chromodynamique quantique (QCD) se prête mal aux méthodes perturbatives, et la simulation directe reste un des meilleurs moyens de sonder la théorie.

Les théories quantiques des champs ont également trouvé de nombreuses applications en physique de la matière condensée^[41],[42]. Des phénomènes tels que la condensation de Bose-Einstein, les plasmas de gaz d'électrons en interaction, certaines phases supraconductives s'expliquent mieux au travers d'une analyse de brisure spontanée de symétrie par exemple. Plus récemment, la découverte de phases topologiques telles que la transition Berezinski-Kosterlitz-Thouless (prix Nobel de physique 2016) et l'étude de l'effet Hall quantique fractionnaire montrent la pertinence des théoriques topologiques des champs quantiques pour l'étude des propriétés de conductivité dans la matière. Les outils développés pour la théorie quantique des champs permettent également d'aborder certains problèmes hors équilibre, par exemple via le formalisme de Keldysh.

• (en) Richard Feynman, The character of physical law, MIT Press, 1964, 184 p. (ISBN 978-0-262-53341-6, OCLC 957554696, lire en ligne)
• Jean Zinn-Justin, Renormalisation et groupe de renormalisation : les infinis en physique microscopique contemporaine, Collège de France, Paris, 1999, 17 p. (lire en ligne)

• Pierre Salati, Introduction à la théorie quantique des champs, Universités de Grenoble Alpes et de Savoie Mont Blanc, 2017-2018 (lire en ligne)
• Jean-Yves Ollitrault, Introduction à la théorie quantique des champs, IPhT, CEA Saclay, 2004-2005 (lire en ligne)
• (en) Tom Lancaster et Stephen Blundell, Quantum Field Theory for the Gifted Amateur, Oxford University Press, 2014, 512 p. (ISBN 978-0-19-151093-9, lire en ligne)
• Michel Le Bellac, Des phénomènes critiques aux champs de jauge, EDP Sciences, coll. « Savoirs Actuels », 1^er janvier 1998, 639 p. (ISBN 978-2-86883-359-4)
• (en) Steven Weinberg, The quantum theory of fields I : Foundations, Cambridge University Press, 1995, 635 p. (ISBN 978-0-521-55001-7, OCLC 31970558, lire en ligne)
• (en) Steven Weinberg, The quantum theory of fields II : Modern applications, Cambridge, Cambridge University Press, 1996, 419 p. (ISBN 0-521-55002-5, lire en ligne)
• (en) Steven Weinberg, The quantum theory of fields III : Supersymmetry, Cambridge University Press, 2005, 442 p. (ISBN 978-0-521-67055-5)
• (en) Anthony Zee, Quantum field theory, as simply as possible, Princeton University Press, 1923, 372 p. (ISBN 978-0-691-17429-7 et 978-0-691-23927-9)

• (en) Frank Wilczek, « Quantum Field Theory », Reviews of Modern Physics, vol. 71, n^o 2,‎ 1^er mars 1999, S85–S95 (ISSN 0034-6861 et 1539-0756, DOI 10.1103/RevModPhys.71.S85, lire en ligne, consulté le 24 mars 2018)
• (en) Silvan Schweber, QED and the men who made it : Dyson, Feynman, Schwinger, and Tomonaga, Princeton University Press, 1994, 732 p. (ISBN 978-0-691-03327-3, OCLC 28966591, lire en ligne)
• (en) Tian Yu Cao, Conceptual developments of 20th century field theories, Cambridge, Cambridge University Press, 1997, 433 p. (ISBN 0-521-43178-6, OCLC 35043034, lire en ligne)

• (en) Gerard 't Hooft, The Conceptual Basis of Quantum Field Theory, 2007 (lire en ligne)
• (en) Meinard Kuhlmann, « Quantum Field Theory », Stanford Encyclopedia of Philosophy,‎ 22 juin 2006 (lire en ligne, consulté le 24 mars 2018)

• Théorie supersymétrique de la dynamique stochastique

• Portail des mathématiques
• Portail de la physique
• Portail des sciences quantiques