Théorie des corps élancés
La théorie de Munk (Munk theory) ou théorie des corps élancés (slender bodies theory) est un modèle visant à expliquer le comportement aérodynamique d’un corps élancé en incidence dans des fluides non visqueux. Plutôt que de se concentrer sur la trajectoire des particules du fluide, cette théorie modélise les échanges de quantité de mouvement entre le corps élancé et le fluide traversé.
Émise en 1921 par Max M. Munk dans un rapport historique[1] du National Advisory Committee for Aeronautics[2], la théorie de Munk conduira à d'importants progrès, notamment dans le calcul de la stabilité aérodynamique des fusées et des missiles en déplacement dans l'atmosphère.
Pour démontrer sa théorie, Munk se base sur l'observation que les dirigeables, alors largement utilisés, doivent déplacer une masse d’air considérable pour se frayer un passage à travers l’atmosphère[3]. En s'appuyant sur la deuxième loi de Newton, il estime les forces impliquées dans ce déplacement massif d'air, permettant ainsi de modéliser les efforts aérodynamiques en jeu.
Principes et hypothèses
Munk, en s’en tenant à l’observation des échanges de quantité de mouvement entre les dirigeables et l’air environnant, a dégagé une méthode de calcul, simple, des efforts de l’air déplacé en réaction à ce déplacement, appliquée aux dirigeables.

Notion de corps élancé
La première hypothèse de Munk fut de considérer qu'un corps dont la pente locale est suffisamment faible, ce qui signifie que les variations de son diamètre par rapport à sa longueur sont faibles. Sa surface extérieure présente ainsi un angle suffisamment faible par rapport à la vitesse du fluide à distance du corps. Une autre définition d’un corps élancé est qu’il est dit ainsi lorsque l’évolution de sa section frontale est très progressive le long de son grand axe, de sorte qu’il ne provoque ni sous-vitesse ni survitesse de l’écoulement à sa surface.
Munk divise ensuite l’air environnant ce corps élancé en tranches normales à son axe, en supposant que l’air est non visqueux.
Une fois cette hypothèse posée, Munk s'intéresse à ce qui se passe dans l’air d’une de ces tranches élémentaires lorsque le corps se déplace d’une longueur élémentaire dx correspondant à son épaisseur. Il considère que les mouvements d’air dus à l’avancée du corps se produisent uniquement à l’intérieur de cette tranche d’air, c'est-à-dire sous forme d’un écoulement bidimensionnel (2D) dans cette tranche. Cela suppose implicitement que le flux d'air généré par chaque tranche n'affecte pas les autres tranches, ce qui est valable si le corps est suffisamment élancé et si ses sections ne varient pas brusquement.[4],[5],[6].
À l'issue de ces réflexions, Munk a calculé que l’effort normal élémentaire suscité par l’incidence sur la tranche du corps dessinée ci-dessus est[7] :
libellé où q est la pression dynamique de l’écoulement, dS est la variation de section du corps élancé sur l’épaisseur de la tranche, etα l’incidence.
Pour les petites incidences (inférieures à 10°), le sinus peut évidemment être pris comme égal à l'angle en radians, ce qui donne :
Exploitations pratiques de ce résultat
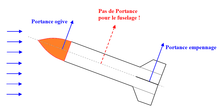
On peut remarquer que lorsque la section du corps reste constante (comme la partie cylindrique médiane d’un dirigeable ou le fuselage de fusée), la force normale de toutes les tranches concernées est nulle. Cette nullité de la portance des parties cylindriques d’un corps est paradoxale pour le néophyte ; par exemple sur l'image ci-contre, il n’est pas naturel de penser que le fuselage cylindrique, bien que placé en incidence par rapport au vent, ne développe pas de portance.
Pourtant ce constat est assez bien vérifié par les mesures en soufflerie, même si les parties cylindriques des fuselages produisent quand-même, aux petits angles d’incidence, une faible portance normale linéaire[8],[9] (voir plus bas à ce sujet la section déroulante "La vraie valeur du des parties cylindriques" ainsi que les articles Stabilité aérodynamique de la fusée et Rapport des Barrowman).
Une deuxième remarque importante est que lorsque l’accroissement de la section élémentaire du corps élancé est positif, la force normale élémentaire est aussi positive (ce qui correspond à une force vers le haut sur les images ci-contre où les corps ont une incidence vers le haut). Dans le cas inverse (accroissement dS négatif) la force normale élémentaire est négative (ce qui est très contre-intuitif).
Il résulte de tout cela que l’intégration des efforts normaux élémentaires au long d’une ogive de fusée, par exemple, résulte en une force normale positive (image ci-dessus). Ce qui implique que lorsqu'une fusée prend de l’incidence, la force normale qui naît sur l’ogive crée un moment d’instabilité par rapport au centre des masses de la fusée (si celui-ci est situé, comme généralement, très en arrière de l'ogive).
De même, la partie avant d'un dirigeable (son ogive) développe pour une incidence positive (vers le haut) une force normale positive (vers le haut).

Par contre, la partie arrière d'un dirigeable, du fait que ses sections normales décroissent, développe une portance négative (une déportance). Cette déportance de la partie arrière du dirigeable, en combinaison avec la portance de la partie avant, va créer un moment déstabilisateur (parfois nommé moment de Munk), moment qui va tendre à augmenter l'incidence du dirigeable (c.-à-d. que si une perturbation atmosphérique place le dirigeable en légère incidence, cette incidence ne va faire que croître jusqu'à placer le dirigeable en travers du vent de sa vitesse). Sur l'image ci-contre, la portance des tranches normales d'un corps à double pointes est représentée par la courbe bleue d'après la théorie des corps élancés. En rouge à marques carrées est la courbe des portances des tranches normales réellement mesurées. Les deux vecteurs bleus représentent la portance de l'avant-corps et la déportance de l'arrière-corps tirées de ces mesures (par intégration). On note que cette dernière déportance mesurée est nettement plus faible que la déportance prédite par la théorie des corps élancés. Appliquée à un corps élancé se terminant par une pointe arrière, la théorie des corps élancés promet en effet une déportance de l'arrière-corps de même module que la portance d'avant-corps. Ces deux forces se composent alors pour créer :
- d'une part une résultante nulle (le corps ne développe donc théoriquement aucune portance lorsqu'il est placé en incidence) ;
- d'autre part le fameux moment de déstabilisation déjà évoqué (ou moment de Munk). Le centre de portance aérodynamique[10] d'un tel corps élancé à pointe arrière se trouve projeté à l'infini avant. Nous verrons plus loin que, d'après les mesures en soufflerie, ce centre de portance, ne se trouve pas à l'infini avant mais quand-même très en avant des corps (dans l'image ci-contre, portance de l'avant-corps et déportance de l'arrière-corps sont composés graphiquement pour dessiner le Centre de portance aérodynamique mesuré du corps). La même composition de ces forces résulte également en une portance (ce qui est vérifié par la portance que développent les dirigeables lorsqu'ils prennent de l'incidence).
Les résultats de la théorie des corps élancés furent très tôt utilisés pour des corps autrement véloces que les dirigeables : les fusées (voir l’article Rapport des Barrowman). Dans l’un de ses textes, H. Julian Allen (qui allait étendre la théorie des corps élancés de Munk aux grandes incidences et aux fluides visqueux) précise d’ailleurs à ce sujet, citant Tsien : « les antiques théories potentielles donnant la répartition de la portance sur les dirigeables sont encore applicables à de tels corps même dans un flux supersonique, pourvu que ces corps soient élancés et à faible incidence[11]. »
Confrontation de la théorie avec les mesures expérimentales


Bien que le raisonnement de Munk fasse appel à beaucoup d’hypothèses simplificatrices, force est de constater que les mesures en soufflerie donnent des résultats tout à fait en accord avec la théorie des corps élancés (surtout pour les avant-corps, nous le verrons à l'instant).
Ainsi, l'image ci-contre compare la distribution des forces normales mesurée sur un modèle de dirigeable à 10° d'incidence (en vert clair) avec la distribution déterminée par la Théorie des corps élancés (en rouge). Pour la partie avant du dirigeable, l'accord est assez bon (sauf au point d'arrêt).
De sorte que les calculs de stabilité aérodynamique des fusées sont toujours basés sur ladite théorie (et même, pour les fusées d'amateurs, dans sa version la plus simple). Deux exemples parlants, à ce sujet, sont la force normale développée par une ogive de fusée et le point d’application de cette force normale : les fuséistes amateurs[14] considèrent la force normale développée par l’ogive comme valant toujours (si est la pression dynamique de l'écoulement, l'incidence de la fusée en radians et la section maximale de l'ogive. Ce qui signifie que le coefficient de force normale de l'ogive est (en référence à la section maximale de l'ogive et par radian), ceci pour des ogives de toutes les formes, y compris l'ogive plate (ou l'absence d'ogive qui donne une tête plate à la fusée) (voir plus bas).

De même, le point d'application de la force normale développée par une ogive est remarquablement bien déterminé par la théorie des corps élancés (la position de cette force normale est donnée dans l'image ci-contre).
D'une façon générale, la position relative de la force normale développée par l'ogive (position nommée XCPA) est donnée par l'équation :
- , et étant le volume, la section maximale et la longueur de l'ogive (cette équation n'est pas donnée dans le rapport des Barrowman mais dans un rapport suivant de James S. Barrowman seul[15],[16]).


En ce qui concerne les arrière-corps, les prédictions de la théorie des corps élancés se montrent moins précises (on l'observe sur la première image de cette section où la déportance arrière est, en ordre de grandeur, la moitié de la portance avant alors que la Théorie des corps élancés la prédit égale à la portance avant). La raison en est que ladite Théorie ne prend pas en compte l’épaisseur de la couche Limite sur la partie arrière des corps profilés (couche limite qui devient très importante, en comparaison avec son épaisseur sur la partie avant)[17]. De sorte que le moment de déstabilisation d'un corps profilé est plus faible que prédit par la théorie.
Une façon d'estimer la déstabilisation d'un corps profilé en incidence est de s'intéresser à son Centre de portance aérodynamique (nommé CPA sur l'image ci-contre à droite et Centre de portance sur l'image ci-contre à gauche)[18] ,[19] : on observe alors que ce CPA est toujours très en avant des corps profilés à faible incidence, parfois même à plus d'une longueur de corps en avant de leur pointe avant (voir à ce sujet l'article Corps de moindre traînée).
L'image de gauche, d'après Hoerner, donne un panorama des Centres de portance (ou CPA) de divers types de corps profilés courants.
Cas particuliers de corps non élancés




L'ogive plate (l'absence d'ogive) ou l'ogive hémisphérique ne sont en rien des corps élancés[20]. Si ces deux ogives très particulières peuvent être considérées comme développant, en ordre de grandeur, un coefficient de force normale d'environ 2 (par radian et en référence à leur section maximale, soit la section de la partie cylindrique qui les suit) (image ci-contre à gauche)[21], le point d'application de cette force normale ne peut être donné par la théorie de Munk.
Pour l'ogive hémisphérique, la logique, comme les données expérimentales recueillies en soufflerie (marques bleu clair sur l'image ci-contre à droite), indiquent que le point d'application de la portance de l'ogive hémisphérique se place en son centre géométrique (donc au centre de sa section maximale)[22],[21].
Quant à l'ogive en tête plate, les mesures en soufflerie placent le point d'application de sa portance notablement en arrière d'elle-même. En tant que disque présenté à l’écoulement, en effet, la tête plate a ceci de particulier qu’elle ne présente aucune surface orientée de façon à transformer une sur- ou sous-pression en force normale. En elle-même, elle ne peut donc développer aucune portance normale. Par contre, toujours pour les faibles incidences, la partie cylindrique du fuselage qui la suit est l’objet d’une forte portance normale[21],[23] (ce qui donne un Cnα de l’ordre de 2,5 par radian, en référence à la section du fuselage cylindrique)[21],[24],[25]. Plus curieusement encore, le point d’application de cette portance normale peut être en arrière de la tête plate de 0,5 à 2,5 diamètres de fuselage.
Évolution de la théorie des corps élancés


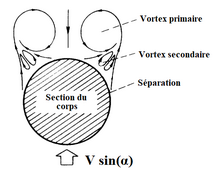

S'appuyant sur les travaux d'autres chercheurs, H. Julian Allen (bientôt accompagné de Edward W. Perkins)[31] a mis en forme une extension aux fluides visqueux (ou réels) de la Théorie des corps élancés de Munk. Dans cette extension, on considère que chaque tranche normale du corps développe, en plus de la force normale dégagée par la Théorie de Munk, une force normale tourbillonnaire naissant du traversier appliqué à cette tranche (cette tranche étant donc assimilée à une tranche de cylindre de même élancement que le corps, au premier régime dans les cas les plus simples (image de droite), la vitesse de cette même tranche étant si est la vitesse de l'écoulement et l'incidence du corps. De fait, les observations d'écoulements sur les corps élancés (image de gauche) dévoilent l'existence de deux nappes tourbillonnaires, ces tourbillons étant relâchés périodiquement dans le sillage desdits corps[32].
Dans le cas simple d'une fusée ogivo-cylindrique en subsonique, par exemple, le total peut alors être approché par la formule :
- Dans ce libellé, le premier terme après le signe égal est bien sûr celui déterminé par la théorie des corps élancés ;
- est l'angle d'incidence (en radians);
- le coefficient donné par la courbe de Goldstein ou celle du NACA RM A50L07, l'élancement du cylindre étant pris comme celui de la fusée[33],[34] ;
- est la surface projetée du corps sur un plan parallèle à son grand axe ;
- et est la surface maximale de l'ogive qui sert ici de référence au .
- Le coefficient apparaissant dans ce libellé est le traversier du cylindre infini en régime sous-critique (ou Premier régime). Il peut être adopté tant que le Nombre de Reynolds diamétral et le Mach transverse, tous deux basés sur la même vitesse transverse , sont inférieurs à respectivement 180 000 et Mach 0,3 ou 0,4 (selon la précision requise)[35]. C'est cette plage de (en fonction du Reynolds et du Mach) que l'on voit sur le graphe 1.
-
 Crédit image:licence CC BY-SA 4.0 🛈Graphe 1
Crédit image:licence CC BY-SA 4.0 🛈Graphe 1
L'extension d'Allen et Perkins permet de prédire, avec prudence, le comportement, pour toutes les incidences possibles, de corps de révolution ou même de sections non circulaires[36].
Aux vitesses supersoniques et pour les élancements supérieurs à 6, l'effet de l'élancement du corps peut être négligé, c.-à-d. qu'on peut prendre (mais le traversier du cylindre infini est très variable avec le Mach et bien supérieur à [37].)
Notes et références
- Les contributions de Max M. Munk ont été jugées si remarquables par le National Advisory Committee for Aeronautics (NACA, le prédécesseur de la NASA) qu'en 1925 cet organisme a publié un article de Joseph Sweetman Ames intitulé A Résumé of the Advances in Theoretical Aerodynamics Made by Max M. Munk. [1]
- (en) Max M. Munk, « THE AERODYNAMIC FORCES ON AIRSHIP HULLS », NACA Report, no 184, (lire en ligne)
- Le Zeppelin Hindenburg déplaçait jusqu’à 248 tonnes d’air à la vitesse maximale de 135 km/h.
- Extension of Lighthill’s slender-body theory to moderate aspect ratios, Zhanle Yu, Christophe Eloy, HAL, [2]
- On peut admettre cette simplification plus facilement si l’on considère que la pente très faible du corps élancé fait que celui-ci se glisse facilement sous les particules d’air en les écartant (diamétralement) mais sans les entraîner en avant.
- (en) H. Julian Allen et Edward W. Perkins, « A study of effects of viscosity on flow over slender inclined bodies of revolution », NACA Report 1048, (lire en ligne [PDF])
- Dans ce résultat n'est pas tenu compte du coefficient multiplicateur (k2 - k1) ; k1 est le coefficient de masse additive pour les déplacements longitudinaux du corps et k2 le coefficient de masse additive pour les déplacements normaux du corps dans le plan de l'incidence. De fait, en 1977, Jorgensen écrira : « Pour les élancements L/D suffisamment grands, il est d'usage de négliger l'effet des masses additives [à savoir le coefficient multiplicateur (k2 - k1) utilisé par Munk dans sa démonstration]. » (en) Howard Jorgensen, « Prediction of static aerodynamic characteristics for slender bodies alone and with lifting surfaces to very high angles of attack », NASA TR R-474, (lire en ligne)
- Le qualificatif linéaire signifie que cette portance est proportionnelle à l'angle d'incidence.
- Cette faible portance normale linéaire du fuselage cylindrique est généralement négligée par les amateurs fuséistes.
- Le centre de portance aérodynamique ou (CPA) est le point d'où il est possible de tenir un corps en incidence sans faire usage d'un moment (en usant uniquement d'une force).
- ESTIMATION OF THE FORCE AND MOMENTS ACTING ON INCLINED BODIES OF REVOLUTION OF HIGH FINENESS RATIO, H. Julian Allen, RM A 9126, [3]
- Cet effet est évoqué p. 32 du texte de Planète-Sciences "Le vol de la fusée, Stabilité et Trajectographie", Juillet 2008 [4], sauf que dans le cas du cône de rétreint, le est négatif, c.-à-d. qu'il va susciter un coefficient d'amortissement négatif, donc un anti-amortissement.
- James Barrowman, qui a présenté ces calculs d'amortissement pour la première fois dans The practical calculation of the aerodynamic characteristics of slender finned vehicles, [5] écrit : "Quand l'incidence varie, la combinaison de la vitesse locale [géométriquement due à cette variation d'incidence] [...] et de la vitesse de l'écoulement produit un angle d'attaque local [différent de l'angle d'attaque pour un corps fixe] [...]".
- En France, ces fuséistes amateurs n'ont le droit de lancer leurs fusées à feu que sous le contrôle de l'association Planète Sciences.
- Barrowman 1967, p. 29
- On la trouve aussi dans le Bonnet et Luneau : A. BONNET et J. LUNEAU, AÉRODYNAMIQUE, THÉORIES DE LA DYNAMIQUE DES FLUIDES, CÉPADUÈS-éditions
- Hoerner écrit d’ailleurs p 19-15 de son ouvrage Lift : « Il apparaît que [l'épaisseur] de la couche limite le long de l’arrière-corps croît avec l’élancement L/D du corps, réduisant par là même les forces normales négatives qui se développent le long de cet arrière-corps […]. En fait, nous pourrions conjecturer que le moment [déstabilisant] pourrait être seulement la moitié du moment théorique pour un rapport D/L ~ zéro [soit un élancement infini]. »
- Ce CPA est appelé par Hoerner et les anglo-saxons, Neutral point, soit Point Neutre : c’est le point d’où l’on peut tenir le corps, à une incidence donnée, sans déployer aucun moment ; c’est donc aussi le point de l’axe où s’applique la résultante des forces aérodynamiques sur le corps à cette incidence.
- Si l'on tient le corps (par une articulation sphérique) en un point de son axe situé en aval de son centre de portance aérodynamique, il aura tendance à prendre de l'incidence ; par contre, si on le tient en amont de ce centre de portance aérodynamique, il fera girouette et manifestera une tendance à se replacer à l'incidence nulle.
- La pente de leur surface est infinie pour l'ogive plate et trop forte, même à l'écart du point d'arrêt pour l'ogive hémisphérique.
- HANDBOOK OF BLUNT-BODY AERODYNAMICS VOL. I, STATIC STABILITY, by J. A. Darling, AD-776-586, Naval Ordinance Laboratory, Silver Spring, MD, DEC 73 [6]
- Le point d'application des forces de pressions d'un hémisphère ne peut être qu'en son centre géométrique.
- Darling note : "La théorie [des corps élancés] ne s'applique pas très bien aux corps d'élancement faible (L/D < 4) parce que l'abruptesse de leur avant-corps exacerbe leur effet aérodynamique sur la partie [cylindrique] qui les suit."
- On peut estimer qu’il y a report du Cnα de la tête plate sur la partie cylindrique qui la suit.
- Comme on le voit sur cette image il se forme en aval de la tête plate (sans incidence) une zone d’eau morte (zone décollée tourbillonnaire) de ~1,5 diamètres.
- Dans la présente réflexion, nous n'évoquerons que les cylindres à base circulaire mais les cylindres à base quelconque sont également justiciables de la théorie des corps élancés...
- LE VOL DE LA FUSÉE 2008
- Hoerner 1985, p. 19-7
- Hoerner 1985, p. 19-9 fig.16
- C'est le Cnα par diamètre de longueur des parties cylindriques, par radian et en référence section du fuselage.
- CHARACTERISTICS OF FLOW OVER INCLINED BODIES OF REVOLUTION, by H. Julian Allen and Edward W. Perkins, NACA RM A50L07 [7]
- Ce lâché de tourbillons se fait symétriquement pour les faibles incidences puis dissymétriquement pour les incidences plus fortes, cette dissymétrie s'approchant de celle existant à l'aval du cylindre dans un écoulement perpendiculaire à son axe, avec création d'un Nombre de Strouhal.
- Jorgensen 1977, p. 9
- Pour la compréhension de cette courbe de Goldstein, voir l'article Ventilation de l'aval du cylindre
- Ces deux conditions sont évidemment respectées plus facilement pour les incidences modérées.
- Jorgensen 1977, p. 11
- Drag of circular cylinders for a wide range of reynolds numbers and ach numbers, F. E. Gowen & E. W. Perkins, NACA TN 2960, 1953 https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930084018.pdf
Bibliographie
- S. F. Hoerner, Résistance à l'avancement dans les fluides, Paris, Gauthier-Villars, (OCLC 727875556, ASIN B07B4HR4HP).
- (en) S. F. Hoerner, Fluid-dynamic drag : theoretical, experimental and statistical information, (OCLC 228216619).
- (en) James S. Barrowman, The theoretical prediction of the center of pressure, Apogeerockets, (lire en ligne).
- Planète Sciences, Le vol de la fusée : Stabilité et Trajectographie, Version 2.0 - juillet 2008, Planète-Sciences, CNES, (lire en ligne)
- (en) Howard Jorgensen, Prediction of static aerodynamic characteristics for slender bodies alone and with lifting surfaces to very high angles of attack, NASA, (lire en ligne)



























