Stabilité aérodynamique de la fusée
La stabilité d’une fusée (et de toutes sortes de mobiles aériens, y compris les véhicules routiers qui fonctionnent aussi dans l'air) est la qualité à ne pas trop dévier de sa trajectoire sous l’effet des perturbations rencontrées sur son chemin. Pour une fusée ou un mobile aérien, lesdites perturbations sont les turbulences de l’atmosphère traversées. En plus de ces perturbations atmosphériques, d’autres défauts peuvent induire des troubles de la stabilité d’une fusée : un désaxement du Centre des Masses (CdM)[n 1] par rapport à la poussée (la poussée ne passant pas par le Centre des Masses) ainsi que des défauts de symétrie des organes aérodynamiques (ogive ou ailerons d'empennage), la poussée ne passant pas par le point d'application des efforts de traînée aérodynamique. Dans la pratique, ces désaxements de la poussée (par rapport au CdM ou au point d'application des efforts de traînée) ne produisent que des écarts de trajectoire assez faibles.
La grande cause de défaut de stabilité d’une fusée est donc d’origine aérodynamique (voir ci-dessous)
Stabilité aérodynamique de la fusée
La stabilité d’une fusée est sa qualité à ne pas trop dévier de la trajectoire qu’on lui a assignée lors de son départ.
Le commun des mortels, longuement formé à l’école de l'expérience quotidienne, pense que pour qu’une fusée lancée verticalement soit stable, il suffit qu’elle soit lestée en bas[réf. nécessaire] (près de sa tuyère), sur le modèle du pendule (qui reste toujours bien vertical). Or c’est l’inverse qui convient (il faut que la fusée soit lourde ‘’en haut’’).

Les lois de la physique indiquent que la condition nécessaire à la stabilité aérodynamique d’une fusée est qu'à l’occasion d’une ‘’embardée’’ angulaire (une rotation accidentelle de l’axe de la fusée par rapport à la tangente à sa trajectoire) cette fusée soit l’objet de forces et de moments qui tendront à corriger cette embardée. Ainsi, dans le schéma ci-contre, l’angle d’embardée fait naître sur la fusée une force aérodynamique dont la composante normale (nommée N sur le schéma) se trouve en un point (nommé CPA, Centre de Portance Aérodynamique) situé en arrière du Centre des Masses de la fusée (CdM) : le moment autour du Centre des Masses qui en résulte fera tourner la fusée de façon à corriger l’embardée (la fusée ne pouvant tourner qu'autour de son Centre des Masses) ; on dit alors que la fusée est stable[réf. nécessaire].
Dans le cas contraire (c.-à-d. lorsque la composante normale se trouve en avant du Centre des Masses) le moment créé par cette résultante va tendre à augmenter l’angle d’embardée initiale, donc les portances et le moment, et ainsi de suite, ce qui mettra la fusée en tête à queue : la fusée est alors dite instable[réf. nécessaire].
Dans le cas de la fusée stable, la correction de l’embardée peut être qualifiée de retour au neutre, même si la fusée, après cette correction de l'embardée, ne retrouve pas tout à fait la même position angulaire qu’avant l’embardée[n 2] : de fait, on peut dire que la fusée n’a qu’une mémoire limitée de sa trajectoire et toutes les perturbations qui vont la mettre en embardées successives (ces perturbations étant les turbulences de l’air) vont plus ou moins la faire dévier de sa trajectoire originelle. Dans la pratique, cependant, et dans le cas d’un lancement vertical sans vent météo, les embardées successives se produisant aléatoirement dans toutes les directions, la fusée dévie peu de la verticale.


Types d’ailerons d’empennage courants
- Ailerons plans :
Les ailerons utilisés pour composer l’empennage des fusées d’amateurs (à feu ou à eau) sont en général des ailerons plans (de simples plaques minces), seulement arrondis à leurs bords d’attaque et de fuite.

- Ailerons ‘‘en formes’’ :
En milieu scolaire et pour les fusées à eau, des ailerons ‘‘en formes’’ peuvent être utilisés. Fabriqués par cartonnage (avec du bristol de boîte de céréales) ils sont faciles à coller sur la jupe de la fusée à eau avec du ruban adhésif. L’image ci-contre à gauche montre une fusée à eau de 0,5 L dotée de tels ailerons.
Ailerons plans et ailerons ‘‘en formes’’ produisent des portances du même ordre de grandeur (à surface et nombre égaux).

- Ailerons multi-tubulaires
À cause de leur ressemblance avec des réacteurs, ce type d’ailerons est souvent apprécié par les concepteurs de fusées à eau. S’agissant d’ailes annulaires cylindriques isolées (c.-à-d. non collées sur un fuselage), Hoerner[1] remarque que pour des élancements supérieurs à ou ( étant la corde ou longueur de ces ailes annulaires et leur diamètre) elles génèrent une portance double de celles des ailes plates (de même projection )[2],[n 3]. Ce constat (très contre-intuitif) peut donc inciter à utiliser les ailes annulaires comme ailerons multiples au bas d'un fuselage, bien que leur CPA propre soit très près de leur bord d’attaque (dans les 10 ou 15% de leur corde ), soit plus vers l'avant (le haut) de la fusée que les 25% des ailerons carrés, par exemple[n 4].
-
 Crédit image:licence CC BY-SA 4.0 🛈Test dans une soufflerie artisanale d'une fusée à eau à empennage multitubulaire.
Crédit image:licence CC BY-SA 4.0 🛈Test dans une soufflerie artisanale d'une fusée à eau à empennage multitubulaire.
- Aile annulaire
Pour les raisons évoquées ci-dessus, l'aile annulaire unique peut être envisagée comme empennage (l'axe de l'aile annulaire unique étant confondu avec l'axe de la fusée). Cette solution a été utilisée pour stabiliser les bombes (cas où la traînée ne constitue pas un problème).
- Panneaux cellulaires
Un dernier type d’ailerons utilisables (pour les fusées à feu ou à eau) est celui des panneaux cellulaires (images ci-dessous). La fabrication des minces cellules de ce type de panneaux est cependant une gageure technique (si l’on veut qu’ils soient assez légers)[n 5].
-
 Crédit image:Steve Jurvetsonlicence CC BY 2.0 🛈Panneaux cellulaires utilisés pour stabiliser aérodynamiquement le premier étage de la Falcon 9 de SpaceX lors de sa redescente.
Crédit image:Steve Jurvetsonlicence CC BY 2.0 🛈Panneaux cellulaires utilisés pour stabiliser aérodynamiquement le premier étage de la Falcon 9 de SpaceX lors de sa redescente. -
 Crédit image:licence CC BY-SA 4.0 🛈Fusée en incidence avec 4 panneaux cellulaires.
Crédit image:licence CC BY-SA 4.0 🛈Fusée en incidence avec 4 panneaux cellulaires.
Calculs de stabilité statique pour deux fusées types
Nous allons ci-dessous mettre en application les principes édictés par le rapport des Barrowman[3]. La publication de Planète Sciences Le vol de la fusée[4] met également en application les mêmes principes, mais sous la forme de formules compactes qui rendent impossible leur bonne compréhension[n 6].
Nous envisagerons ci-dessous le cas d'une fusée à feu subsonique type (dotée d'une ogive conique, d'un fuselage cylindrique et d'un empennage de 3 ou 4 ailerons carrés dont l'envergure unitaire est égale au diamètre du fuselage). Nous envisagerons également le cas d'une fusée à eau type (nécessairement subsonique) de même silhouette générale que la fusée à feu précédente, mais dotée d'une ogive biconique (plus classique dans ce genre de réalisation). Il est sans doute utile de répéter ici que les lois de l'aérodynamique sont les mêmes pour les fusées à eau et pour les fusées à feu (ici subsoniques).
Les calculs présentés ci-dessous n'évaluent que la stabilité statique de la fusée, cette stabilité statique étant définie comme la tendance d'une fusée à revenir à sa position neutre (c.-à-d. alignée sur sa trajectoire) après une perturbation. Il faut noter que cette tendance est la tendance instantanée mais que les calculs de stabilité statique ne renseignent pas sur la vitesse avec laquelle le retour au neutre va se produire : cette vitesse de retour au neutre (et les oscillations qui s'ensuivent) relève des calculs de stabilité dynamique qui seront abordés en fin d'article.
Rappelons que dans la méthode des Barrowman, un fuselage cylindrique est censé ne produire qu'une portance négligeable (cette simplification est acceptable en première approximation).

Les fuséistes utilisent pour leurs calculs le coefficient de force normale et le coefficient de force axiale (tous deux en rouge sur l'image ci-contre).
- La force normale est la projection sur un plan normal à l'axe de l'engin de la résultante aérodynamique développée par le fuselage ou un organe aérodynamique.
- La force axiale est la projection sur l'axe de l'engin de la résultante aérodynamique développée par le fuselage ou un organe.
Le coefficient de force normale est défini comme :
- libellé où est la portance normale de l'organe considéré (en Newton), la pression dynamique de l'écoulement, l'angle d'incidence de cet organe en radians et la surface de référence adoptée pour le calcul de ce .
Il faut prendre conscience que les coefficients et des fuséistes sont établis en repère corps (c.-à-d. en repère fusée, à savoir l'axe de la fusée) alors que les coefficients et des avionneurs sont établis en repère vent (la direction de ce vent n'étant autre que la trajectoire de l'avion ou la direction du vent dans la soufflerie qui a testé son modèle). C'est ce que l'on peut observer sur l'image ci-contre.
La surface de référence utilisée dans l'établissement du et du est fréquemment la maîtresse section du fuselage de l'engin (dans le cas d'une fusée simple la section de l'ogive) . Cependant, comme toujours en Mécanique des fluides, le choix de la surface de référence est libre : la seule obligation impérative est de toujours préciser ce choix (il faut toujours penser qu'il n'y a jamais de surface de référence évidente).
Ce qui rend pratique l'usage des coefficients fuséistes et , c'est que le d'un engin (ou d'un de ses organes) ne peut avoir aucun effet directionnel sur cet engin (ce qui n'est pas le cas du lorsque l'incidence est non nulle[n 7]).
Les coefficients fuséistes et sont évidemment liés aux coefficient des avionneurs et [n 8] par des formules simples de conversions (pourvu que la même surface de référence soit utilisée pour tous ces coefficients). Ces formules de conversion sont :
- et :
Et dans l’autre sens :
- et :
Voir aussi l'article la section Coefficients de l'article Aérodynamique.
Portance de l’ogive de la fusée à feu type

L'ogive d'une fusée constitue son avant-corps. Sa fonction est de caréner le fuselage qui le suit (en produisant une traînée aérodynamique raisonnable[n 9]). Cependant, cet avant-corps (l'ogive), lorsqu'il est placé en incidence (à l'occasion d'une embardée angulaire de la fusée) développe une portance mal placée qui va déstabiliser la fusée.
Pour les incidences faibles (inférieures à 10°), les ogives, en vertu de la Théorie des corps élancés (théorie que l'on doit à Max M. Munk[5]) présentent toutes un coefficient de force normale [n 10] de par radian (en référence à leur surface frontale, soit si est le grand diamètre de cette ogive). C'est-à-dire que pour une incidence d’un dixième de radian (5,73°), cette ogive développe une force normale de , étant la pression dynamique de l’écoulement. Retenons que quelle que soit leur forme (conique, parabolique, gothique tangente ou non, toutes les ogives suscitent la même portance et donc le même Coefficient de force normale de par radian (en référence à la surface frontale de l'ogive). Ceci est d'ailleurs encore vrai, en ordre de grandeur, pour l'absence d'ogive (la tête plate).
Il convient ici (pour faciliter la suite du calcul) de faire appel à la notion de Surface Équivalente de Portance ; Cette Surface Équivalente de Portance n'est autre que le produit du par la surface qui a présidé au calcul de ce . La "Surface Équivalente de Portance" est donc le pendant, pour les portances, du parfois utilisé pour la traînée. Elle s'exprime en m² et l'on n'a plus qu'à la multiplier par la pression dynamique et l'incidence en radians pour obtenir la force de Portance (en Newton).
Dans ces conditions, la Surface Équivalente de Portance de l'ogive est , étant le grand diamètre de cette ogive.
Point d’application de la portance de l’ogive de la fusée à feu type

Le point d’application de la portance normale que génèrent les ogives est donné par la Théorie des corps élancés. Ce point d'application dépend de la forme des ogives. Pour l'ogive conique de notre fusée type, il est situé au 2/3 de la longueur de cette ogive. On dit donc que le XCPA propre de l’ogive est aux 2/3 de sa longueur. Le tableau ci-contre donne le XCPA propre d’autres formes d’ogives (le XCPA propre d’une ogive étant mesuré depuis sa pointe avant)[n 11].
D'une façon générale, la position relative du XCPA de l'ogive est donnée par l'équation :
, et étant le volume et la section maximale de l'ogive (cette équation n'est pas donnée dans le rapport des Barrowman mais dans un rapport suivant de James S. Barrowman seul[6],[n 12]).
Portance de l'empennage de la fusée à feu type
La portance des ailerons d'empennage est calculable par la formule de Diederich[7],[n 13],[n 14], laquelle est réservée aux ailes de faible envergure (ce qui est le cas des ailerons de fusées). Dans le cas simplifié d'une aile rectangulaire ou carrée (c.-à-d. sans flèche), la formule de Diederich se simplifie en :
- étant l'allongement efficace de l'aile (nous le définissons ci-dessous).
Pour les ailes d' allongement efficace allant de 1 à 2, cette formule peut être linéarisée en : les ailerons de fusée dépassant rarement l'allongement efficace de 2, cette formulation simplifiée pourrait être utile au collège[n 15].
L'allongement géométrique [n 16] d'une aile rectangulaire est, par définition, le rapport de son envergure sur sa corde, soit .
Pour une aile de forme quelconque, cette définition devient , étant toujours l'envergure unitaire (l'envergure d'un seul aileron) et étant la surface de l'aile[n 17].
Mais la formule de Diederich est basée sur des mesures de portance d'ailes isolée (en l'absence de fuselage). Or dans le cas d'un aileron d'empennage, la présence du fuselage produit deux effets :
- Un surflux sur les ailerons du fait que l'obstacle que constitue le fuselage détourne une partie de l'écoulement vers les ailerons (nous y revenons à l'instant);
- Un effet de paroi qui double l'allongement de l'aileron, le fuselage se comportant comme une cloison plane d'extrémité qui transforme l'écoulement autour de l'emplanture en un écoulement 2D[n 18]
La conclusion (notable) qu'il faut tirer de ce constat de la présence du fuselage est que l'allongement géométrique des ailerons de fusées doit toujours être multiplié par deux pour obtenir leur allongement efficace dans la formule de Diederich ci-dessus. Les Barrowman écrivent d'ailleurs (sans autres explications) :
, étant toujours l'envergure unitaire (l'envergure d'un seul aileron) et étant la surface de l'aile.
Il en ressort que la formule de Diederich dote chaque aileron carré d'un de 2.60 (toujours par radian et en référence à sa surface portante ).
Ceci établi, il convient encore de tenir compte dans l'évaluation de la portance des ailerons d'un coefficient d'interactions (interactions des ailerons sur le fuselage et du fuselage sur les ailerons). L'expérience démontre qu'on doit pondérer le précédemment établi pour un aileron par le coefficient multiplicateur :
étant toujours l'envergure unitaire (l'envergure d'un seul aileron) et le diamètre du fuselage au droit des ailerons.
Dans le cas de notre fusée type, , ce qui donne un coefficient d'interactions de 1,33. Il en résulte que chaque aileron présente un de 2,60*1,33 = 3,46.
La surface équivalente de portance de cet unique aileron[n 19] est alors 3,46
Nombre d'ailerons de la fusée à feu type participant à la stabilité

Dans le cas de notre fusée type possédant 4 ailerons, on considère que seuls deux ailerons sont placés en incidence lors d'une embardée de la fusée (les deux autres ailerons ne prenant pas d'incidence). De fait, dans l'image ci-contre, où l'empennage se présente "en " lors d'un embardée dans le plan horizontal, on comprend que seuls les deux ailerons gris prennent de l'incidence. Lorsque l'empennage se présente "en X", on considère que la portance que développeront les 4 ailerons sera de même valeur que les deux ailerons travaillant lors d'une présentation "en ". Autrement dit, pour une incidence donnée, la portance développée par un empennage de quatre ailerons est la même quelle que soit la présentation en roulis (en ou en X, ou tout autre présentation intermédiaire).
Il en résulte que c'est la portance de deux ailerons (ces ailerons étant dans le même plan) qui doit être quantifiée pour juger de la stabilité d'une fusée dotée de quatre ailerons.
Ceci étant, plutôt que de multiplier par 2 le d'un aileron (dans le cas d'un empennage de 4 ailerons), il est plus intéressant de multiplier par , car l'expérience démontre qu'un empennage de 3 ailerons produit 1,5 fois le d'un seul aileron : On pourra donc donner à sa valeur 4 ou 3 selon que la fusée arbore 4 ou 3 ailerons.
Si une fusée est dotée de 6 ailerons carrés à l'envergure unitaire valant toujours un diamètre de fusée, on pourra considérer que ces 6 ailerons se comportent comme 5,25 ailerons (c.-à-d. qu'on peut calculer la portance de l'empennage en donnant la valeur 5,25 au nombre d'ailerons[9],[n 20],[n 21],[n 22].
Conclusion pour la portance de l'empennage de la fusée à feu type
Il résulte de tout ce qui vient d'être dit que le coefficient de portance de l'empennage de notre fusée type est :
Il en résulte que de l'empennage de notre fusée type à quatre ailerons peut être évalué à :
(ce étant établi en référence à la surface unitaire d'un aileron.
Point d'application de la portance de l'empennage de la fusée à feu type
Cas des ailerons rectangulaires ou carrés
On considère qu'aux petits angles d'incidence rencontrés lors du vol d'une fusée convenablement conçue, le CPA (point d'application de la portance) d'ailerons rectangulaires ou carrés est situé au 25 % de leur corde.
Point d'application de la portance totale de la fusée à feu type

Les deux portances en jeu dans le vol de cette fusée type sont donc à présent connues. Le point d'application de leur résultante est alors facilement calculable par calcul de leur moment autour d'un point quelconque[n 23] (image de gauche).

On peut aussi, si l'on désire éviter les calculs, utiliser la méthode de composition graphique des deux portances (image de droite composant deux forces de modules 2 et 4). Cette méthode graphique consiste à intervertir l'emplacement des deux forces en inversant l'une d'elles (ce qui donne la construction fuchsia). Le point d'application de la résultante (de module 6) est ainsi trouvé.
Ainsi, pour une ogive de 155 mm de longueur et une hauteur totale de la fusée de 490 mm, le CPA total de la fusée se place à 365,3 mm de la pointe de l'ogive.
Stabilité aérodynamique d'une fusée à eau type

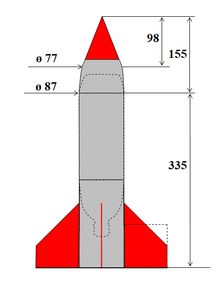
Le schéma ci-contre donne la silhouette de ce qu'on pourrait nommer une fusée type. Cette fusée est construite à partir de deux bouteilles de 1,5 L d'une boisson gazeuse[n 24]. L'une des bouteilles est conservée intègre et sert de réservoir et de moteur à la fusée. L'ogive qui vient caréner ce moteur est formée du haut de la deuxième bouteille coiffée d'un cône de papier enroulé et collé. Les quatre ailerons d'empennage sont montés sur une jupe tirée de la partie centrale (à peu près cylindrique) de la même deuxième bouteille. Ces ailerons sont carrés et leur envergure est égale au diamètre de la fusée.
Nous allons donner ici la valeur des coefficients de force normale des deux éléments aérodynamiques à prendre en compte, à savoir l'ogive et l'empennage.

Portance de l'ogive de la fusée à eau type
Comme le montre l'image ci-contre, cette ogive est biconique, sa partie blanche (un cône de papier enroulé) se raccordant avec une partie tronconique.
Nous avons dit plus haut que toutes les ogives suscitent la même portance et donc le même Coefficient de force normale de par radian (en référence à la surface frontale de l'ogive).
La Surface Équivalente de Portance de l'ogive (celle-ci étant définie plus haut) est donc , étant le grand diamètre de cette ogive (87 mm ici).
Point d'application de la portance de l'ogive de la fusée à eau type
Le point d'application de la portance de l'ogive peut être calculé par les formules données dans Le vol de la fusée[4], ce calcul prenant en compte la partie conique supérieure ainsi que la partie tronconique inférieure. Ce calcul place le XCPA de cette ogive biconique à 50% de sa longueur (qui est de 155 mm), soit 77,5 mm.
Portance des ailerons et point d'application de cette portance
La surface équivalente de portance des ailerons carrés (leur envergure unitaire étant le diamètre de la fusée), ainsi que leur XCPA propre sont les mêmes que pour la fusée à feu type (valeurs données plus haut). Le XCPA de ces ailerons se trouve donc à ~ 425 mm de la pointe de l'ogive.
Point d'application de la portance totale de la fusée à eau type
La composition des deux portances (celle de l'ogive et celle de l'empennage) place le CPA total de cette fusée à eau type à 360,5 mm de la pointe de son ogive.
Autre forme d’ailerons
Si les ailerons carrés ou rectangulaires, en subsonique, offrent la meilleure portance (à surface donnée), il leur manque cette esthétique de la vitesse que peut donner la flèche du bord d’attaque[n 25].
En faisant pivoter à 45° le bord d’attaque d’un aileron carré autour de son point milieu (image ci-contre), on ne change pas sa surface. Par contre, son (le Coefficient de portance normale d’un aileron, en référence à sa surface unitaire) n’est plus de 2,60 mais de 2,51 (un peu plus faible, donc). L’action du coefficient d’interactions (qui est inchangé), ainsi que la prise en compte du nombre d’ailerons (4 dans notre exemple) font que la surface équivalente de portance de cet empennage de 4 ailerons en flèche vaut : .
Le XCPA propre d’un aileron peut être calculé[10] comme étant à 45,83% de l’avant de son emplanture (soit 5,4 mm plus haut que celui de l’aileron carré de même surface). Il en résulte que le CPA de cette fusée à 4 ailerons en flèche de surface unitaire [n 26] est situé à 354,3 mm de la pointe de l’ogive (au lieu de 360,5 mm pour 4 ailerons carrés de même surface).
Cas général des ailerons de forme trapézoïdale

Pour des ailerons trapézoïdaux (le rectangle, le carré, les parallélogrammes et les triangles sont des trapèzes particuliers) le CPA est toujours situé sur la ligne des 25 % des cordes. D'autre part, il est situé, en envergure[n 27] à la même distance que le barycentre de la surface de l'aileron[n 28].
Pour des ailerons en forme de parallélogramme (en flèche ou non), le CPA est donc à mi-envergure sur la ligne des quarts de cordes.
Pour des ailerons trapézoïdaux la position du CPA est donné dans Le vol de la fusée[11], soit par une méthode graphique, soit par une formule arithmétique.
La grande variabilité du Centre des Masses de la fusée à eau

Durant sa phase propulsive, la fusée voit évidemment le volume de l’eau emportée décroître jusqu’à zéro (c'est également la même chose pour le carburant -liquide ou solide- des fusées à feu). À la moitié de la propulsion, la masse d’eau restante se trouvant en quantité assez importante assez près de la tuyère, elle peut être très déstabilisante. Il n’est alors pas rare que la fusée fasse montre d’un court épisode d’instabilité transitoire, cet épisode prenant fin dès que toute l’eau a été éjectée (la fusée ‘’à sec’’ redevenant stable) : ce défaut de stabilité transitoire se traduira donc, après un début de trajectoire tendu (en début de propulsion), par une trajectoire à courbure marquée (instabilité transitoire), laquelle sera suivie d’une trajectoire à nouveau tendue (bonne stabilité à sec), évidemment dans le prolongement de l'orientation suscitée par l'instabilité transitoire. Une façon de corriger ce problème d’instabilité transitoire est évidemment de lester l’ogive. Outre son utilité pratique, le lestage de l'ogive offre évidemment un grand intérêt pédagogique (spécialement en milieu scolaire) puisqu'il inscrit dans la mémoire des fuséistes débutants que, très contre intuitivement, la fusée gagne en stabilité à être plus lourde en haut[n 29].
L’image ci-contre montre l’évolution du Centre des Masses d’une fusée à eau ‘’type’’ de 2 L de volume[n 30]. La courbe rouge représente l’évolution de la hauteur du Centre des Masses de la fusée complète en fonction du temps : on note que ce Centre des Masses passe par un point bas qui peut être générateur d’instabilité transitoire (selon la position du Centre des Masses à sec, donc du lestage éventuel de l’ogive, et la position du CPA total de la fusée -symbolisée par l'horizontale tiretée verte-). Sur ce graphe, les courbes tiretées rouge, bleu dense et bleu clair représentent des hauteurs calculées pour une fusée à eau immobile (au banc d'essais) puisque alors la hauteur de l'eau dans la fusée ne subit pas d'accélération. Les courbes de mêmes couleurs en trait plein ont, par contre, été calculées en tenant compte de la hauteur de la colonne d'eau dans la fusée accélérée.
La stabilité dynamique des fusées

Les calculs ci-dessus traitent de la stabilité statique de la fusée. On peut les voir comme l'étude, sur une photographie, des efforts auxquels la fusée est soumise (à l'incidence où la fusée a été photographiée). L'étude de stabilité dynamique est au contraire consacrée à la vitesse (très variable) à laquelle vont se produire les mouvements de la fusée sous les efforts calculés par l'étude de stabilité statique. La stabilité dynamique va donc permettre de dessiner le film du vol de la fusée, avec ses oscillations de retour au neutre plus ou moins rapides. Comme le montre l'animation ci-contre, les efforts aérodynamiques agissant sur la fusée varient en continu (selon la vitesse du vent ressentie par la fusée et son incidence instantanée).
Facteurs d'amortissement
Dans la pratique, le retour au neutre de la fusée (lorsque celle-ci est mise en incidence par une turbulence de l'atmosphère) se fait après un certain nombre d'oscillations d'amplitudes décroissantes. Le nombre de ces oscillations est d'autant plus réduit qu'existent dans le mouvement de la fusée un certain nombre de facteurs d'amortissement : La vitesse locale de l'air sur l'ogive et les ailerons d'empennage (cette vitesse étant la composition de la vitesse de la fusée sur sa trajectoire et de la vitesse locale propre induite par les oscillations) procure un premier amortissement (c'est finalement l'amortissement qu'on peut observer lorsque l'on écarte une girouette du lit du vent). Un amortissement complémentaire est créé, pendant le phase propulsive, par le mouvement rapide de la matière éjectée. Cet amortissement par éjection de masse[12](Jet damping , en anglais) existe aussi avec les fusées à eau. Par contre, dans le cas particulier d'une fusée dont le fuselage possède des rétreints[n 31], il faut noter que ces rétreints apportent un coefficient d'amortissement négatif.
Influence du nombre de Mach

En première approximation, la stabilité d'une fusée type tend à être augmentée aux abords de la vitesse du son et au-delà ((augmentation du total de la fusée et recul de son total)[13]. Bien sûr, ce scrupule ne vaut pas pour une fusée à eau...
L'image ci-contre donne la position du (position nommée ici ) selon la taille des ailerons et selon le Nombre de Mach. La courbe la plus basse (celle qui donne la meilleure stabilité) concerne une fusée à ailerons d'envergure un peu plus faible que celle de nos fusées types (envergure de ). On voit qu'à mesure que la taille des ailerons croît, ceux-ci tendent à contrer l'effet du Nombre de Mach sur le fuselage seul (effet principalement dû à l'ogive)[14].
Bibliographie
- (en) James S. and Judith A. Barrowman, The theoretical prediction of the center of pressure, Apogeerockets, (lire en ligne).
- (en) James S. Barrowman, The practical calculation of the aerodynamic characteristics of slender finned vehicles, NASA, (lire en ligne)
- Planète Sciences, Le vol de la fusée : Stabilité et Trajectographie, Version 2.0 - juillet 2008, Planète-Sciences, CNES, (lire en ligne)
- S. F. Hoerner, Résistance à l'avancement dans les fluides, Paris, Gauthier-Villars, (OCLC 727875556, ASIN B07B4HR4HP).
- (en) S. F. Hoerner, Fluid-dynamic drag : theoretical, experimental and statistical information, (OCLC 228216619).
- A. Bonnet et J. Luneau, AÉRODYNAMIQUE, THÉORIES DE LA DYNAMIQUE DES FLUIDES, CÉPADUÈS-éditions
Voir aussi
Articles connexes
- Aérodynamique : Portance et Traînée
- Confusion de la fusée pendulaire
- Rapport des Barrowman
- Théorie des corps élancés
- Fusée à eau
Notes
- ↑ Le Centre des Masses est le barycentre de toutes les masses de la fusée, ce barycentre étant communément dénommé Centre de Gravité ; cependant, la gravité n’intervenant aucunement dans la stabilité de la fusée, il est plus rigoureux de nommer ce barycentre Centre des Masses ou Centre des Inerties.
- ↑ En fait, la fusée ne revient au neutre qu’après une série d’oscillations ; l’étude de ces oscillations constitue le domaine de la Stabilité Dynamique.
- ↑ La surface de friction de telles ailes annulaires est cependant fois plus forte que celle de l'aile plate de même projection.>
- ↑ Pour Hoerner, la surface équivalente de portance par radian d'incidence (soit le rapport , étant la pression dynamique et étant l’incidence en radians) des ailes annulaires d'élancement supérieurs à ou peut être prise comme , soit si est la section interne de l’aile annulaire. Cette valeur est indépendante, il faut le noter, de la corde de l’aile annulaire, ce qui est très contre-intuitif. Cette même valeur est confirmée par le NACA TN 4117 de Fletcher : Experimental investigation of lift, drag, and pitching moment of five annular airfoils, Herman S. Fletcher [1].
- ↑ Les panneaux cellulaires ne stabilisent pas la fusée en produisant de la traînée aérodynamique, comme il est souvent pensé, mais ils produisent bien de la portance (en déviant le flux d’air passant dans toutes les cellules qui les composent ainsi qu’en déviant le flux passant à l’extérieur de leur cadre).
- ↑ Cet ouvrage est néanmoins essentiel et comporte énormément d'informations sur la stabilité des fusées.
- ↑ Sauf position particulière du Centre des masses.
- ↑ Nous ne traitons ici, pour simplifier, que le cas des trajectoires dans un plan vertical, donc des trajectoires 2D.
- ↑ Pour cette question du Cx propre des ogives, voir la section Avant-corps de fusées de l'article Avant-corps (mécanique des fluides).
- ↑ Le coefficient de force normale représente pour les aérodynamiciens la capacité d'un élément aérodynamique d'une certaine section (l'ogive, ici) à développer de la portance sous l'effet de la vitesse et de l'incidence.
- ↑ Le XCPA propre de l’ogive sphérique (encore nommée ogive hémisphérique) est à 100 % de sa longueur, contrairement à ce que prédit la Théorie des corps élancés qui ne peut convenir à ce corps typiquement non élancé.
- ↑ On la trouve aussi dans le Bonnet et Luneau : A. BONNET et J. LUNEAU, AÉRODYNAMIQUE, THÉORIES DE LA DYNAMIQUE DES FLUIDES, CÉPADUÈS-éditions
- ↑ Cette formule semi empirique donne une assez bonne quantification de la portance des ailes de très faible allongement et de toutes formes, sauf, d’après Bonnet et Luneau, pour les ailes delta[8]
- ↑ On trouve d'autres formulations sous la plume d'Hoerner ainsi que celle de Wicker et Fehlner.
- ↑ Une linéarisation plus simple pour les faibles allongements efficaces est citée par Diederich lui-même, c'est : . Elle semble fidèle pour les allongements efficaces inférieurs à 1.
- ↑ Cet allongement est encore nommé Rapport d'Aspect.
- ↑ Cette définition est évidemment valide pour l'aile rectangulaire.
- ↑ ...alors que sans le fuselage se formerait à cette emplanture des tourbillons marginaux classiques, soit un écoulement typiquement 3D.
- ↑ Nous avons défini déjà cette Surface équivalente de Portance pour l'ogive. Elle s'exprime en m² et l'on n'a plus qu'à la multiplier par la pression dynamique et l'incidence en radians pour obtenir la force de Portance (en Newton).
- ↑ Cette valeur de 5,25 vaut pour des ailerons dont l'envergure unitaire égale un diamètre de fuselage. Elle dépend très légèrement de cette envergure (relativement au diamètre du fuselage).
- ↑ On note donc que l'efficacité des ailerons décroît lorsque leur nombre est supérieur à 4 ; ceci s'explique par les interactions qui se font entre ces ailerons trop nombreux.
- ↑ Le Military Handbook donne, quant à lui, p. 5-24, un nombre efficace d'ailerons de 5,48 pour 6 ailerons et 6,48 pour 8 ailerons, ceci sans évoquer l'envergure de ces ailerons (relativement au diamètre du fuselage). MILITARY HANDBOOK, DESIGN OF AERODYNAMICALLY STABILIZED FREE ROCKETS, MIL-HDBK-762(MI) [2]
- ↑ En fuséologie amateur, la tradition est de calculer ces moments par rapport à la pointe de l'ogive.
- ↑ Ces deux bouteilles sont les anciennes bouteilles de Coca Cola 1,5L. Si la marque historique a abandonné cette bouteille, elle a été reprise par un certain nombre de fabricants de boissons gazeuses, dont Breizh Cola ainsi que plusieurs fabricants de cidre.
- ↑ On peut aussi apprécier que le moment fléchissant que crée la portance soit supporté par une emplanture plus longue.
- ↑ si est le diamètre de la partie cylindrique du fuselage.
- ↑ c.-à-d. perpendiculairement à l'emplanture d'un aileron...
- ↑ La position du barycentre d'un trapèze est donné par une formule, mais il peut être valablement déterminé en cherchant le point d'équilibre d'un modèle d'aileron en bristol.
- ↑ Pour des raisons de sécurité ce lest ne doit pas être un caillou ou une pièce métallique mais il doit être fait de pâte à modeler ou, par défaut, d’argile humide
- ↑ Ce volume est le volume ‘’nominal’’ de la boisson que renfermait la bouteille avant qu’elle devienne le réacteur d'une fusée à eau.
- ↑ Un rétreint est une partie tronconique de sections décroissantes vers l'arrière de la fusée.
Références
- ↑ Hoerner 1965, p. 132.
- ↑ Hoerner 1965, p. 136
- ↑ BarrowmanReport 1966, p. 1-43
- Le vol de la fusée 2008
- ↑ (en) Max M. MUNK, The Aerodynamic Forces on Airship Hulls, NACA REPORT No. 184, NACA, (lire en ligne)
- ↑ Barrowman 1967, p. 29
- ↑ (en) Franklin W. DIEDERICH, A PLAN-FORM PARAMETER FOR CORRELATING CERTAIN AERODYNAMIC CHARACTERISTICS OF SWEPT WINGS, NACA TECHNICAL NOTE 2335, NACA,
- ↑ Bonnet et Luneau.
- ↑ Calculating the center of pressure of a model rocket, by James Barrowman, Technical information report N° 33 (TIR-33), [3]
- ↑ Vol de la fusée 2008, p. 22.
- ↑ Le vol de la fusée 2008, p. 22
- ↑ Vol de la fusée 2008, p. 32.
- ↑ Fusée expérimentale DENEB, dossier technique, ISAE ENSMA, [4]
- ↑ The effect of low aspect ratio rectangular and delta cruciform fins on the stability of bodies of revolution with tangent ogives at small angles of attack through a Mach number range of 0 to 3.5, by Clark De Jonge, Armed Services Technical Information Agency, AD 278 423 [5]































![{\displaystyle C_{N\alpha Og}\;[\pi D^{2}/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30bcb2faebb0ba71b5eb4e58b0dac40e6ba6b05)























![{\displaystyle 2\;[\pi D^{2}/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e52ca688d4558a0d2f127cce8b67c771fd65e71)










