Ventilation de l'aval du cylindre

La ventilation de l’aval d'un cylindre de longueur finie (présentée en travers d’un écoulement) est, en mécanique des fluides, un courant venant d’une face plane du cylindre pour nourrir la zone dépressionnaire existante à son aval. Cette zone d’eau morte étant le siège de tourbillons alternés (allée de tourbillons de Bénard-Karman), le courant de ventilation s'insère à l’intérieur de l’allée (l’espace entre les deux suites de tourbillons). Le courant de ventilation se propage très loin des extrémités du cylindre (jusqu’à 20 ou 30 diamètres de chaque extrémité[1]) en diminuant notablement son coefficient de traînée .
En anglais, pour décrire ce phénomène, le terme « ventilation » est également utilisé par Sighard F. Hoerner [2], bien que le terme le plus fréquent soit « downwash ».
La ventilation de l’aval du cylindre peut s’observer à la salissure des cheminées provenant des fumées ; en effet, bien que ces fumées soient mues d’une certaine vitesse verticale, le vent météorologique, après s’y être mélangé, les entraîne vers le bas du fait de cette ventilation.
Corps concernés

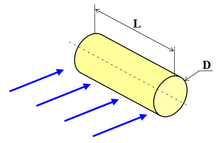
Tous les cylindres, quelle que soit leur section (circulaire, elliptique, carrée à angles vifs ou carrée à angles arrondis) connaissent une ventilation de leur aval lorsqu'ils sont placés en travers d'un écoulement, soit à angle droit, soit même à des angles plus faibles. Les corps non cylindriques (donc à génératrices non rectilignes) comme les fuselages connaissent également une ventilation de leur aval.
L'écoulement du vent météo sur les tours d'habitation donne lieu à une ventilation de leur aval. En cas de tempête, les mouvements (élastiques) qui en résultent, conjugués avec le déversement des tourbillons de Bénard-Karman classiques, peuvent nuire au confort dans les étages les plus élevés[réf. nécessaire].
Si la palette infinie (ou plaque plane d'une certaine largeur H et de longueur L infinie) exposée frontalement à un écoulement montre un de 2, une portion de palette de longueur non infinie, toujours présentée frontalement, connaît également une ventilation de son aval depuis chacune de ses extrémités. À mesure que sa longueur L décroît, son diminue pour atteindre 1,17 lorsque L = H (plaque carrée)[n 1][réf. nécessaire].
Conséquence de la ventilation de l'aval du cylindre

Ainsi que déterminé en 1938 par Sydney Goldstein[3], la ventilation diminue notablement le frontal des cylindres et palettes de longueur finie placés en travers d'un écoulement (les cylindres sont ici à un Reynolds correspondant à leur premier régime).
Les ordonnées de ces courbes représentent le quotient η (prononcer êta) du d'un corps de longueur finie sur le du même corps de longueur infinie (ce quotient η est toujours inférieur à 1). On lit, par exemple, sur ce graphe que si le frontal d'un cylindre circulaire infini au premier régime est ~1,2, celui d'un cylindre d'élancement L/D = 4, par exemple, est à peu près (courbe rouge).
Une telle diminution n'est pas surprenante en mécanique des fluides[réf. nécessaire] puisque le des corps suscitant un écoulement 3D est toujours beaucoup plus faible que le des corps suscitant un écoulement 2D, ceci parce qu'un corps suscitant un écoulement 3D offre toujours plus de voies à son contournement par le fluide qu'un corps suscitant un écoulement 2D[n 2] : le d'un cylindre court est donc plus faible que celui du cylindre infini[réf. nécessaire].
En 1950, Harry Julian Allen tira de l'observation de ce phénomène une règle empirique permettant de calculer la portance normale des fuselages (de fusées ou d'avion) aux fortes incidences (alors que l'on ne savait calculer auparavant leur portance normale qu'aux faibles incidences selon la méthode linéaire des Barrowman)[4]. La méthode d'Allen[n 3] consiste à calculer la portance normale des fuselages comme la somme de leur portance linéaire[n 4] et de leur portance tourbillonnaire (qui tient compte de la ventilation). La contribution de cette dernière devient prépondérante aux fortes incidences.
Une question se pose, à la lecture du graphe de Goldstein[réf. nécessaire] : peut-on trouver une régression logique à ces courbes du η ? Cette régression logique existe ; pour la trouver, par exemple à propos des cylindres, il suffit de se placer dans le cas du plus long cylindre d'élancement λ dont la partie centrale est concernée par la ventilation (sous-entendu : si l'on allonge ce cylindre par un tronçon médian, l'écoulement sur ce tronçon médian ne sera plus concerné par la ventilation, son écoulement étant strictement 2D et son Cx local 1,2 au premier régime). En poursuivant le raisonnement, on trouve que la régression logique est une hyperbole d'équation :
η = 1 - λ(1-η)/λ
où λ et η sont l'élancement et l'êta du plus long cylindre concerné par la ventilation et, bien sûr, λ et η l'abscisse et l'ordonnée d'un cylindre quelconque plus long que le cylindre dont la partie centrale est encore touchée par la ventilation.
Hoerner, dans son ouvrage Fluid-Dynamic Drag[2] (p. 52), suggère à l'issue d'une méthode graphique que cette hyperbole pourrait être (pour le cylindre fini) :
η = 1 -5/λ
Cependant, la courbe d'Hoerner présente quelques écarts par rapport à celle de Goldstein[réf. nécessaire][n 5]. D'autre part, la méthode graphique utilisée par Hoerner pour déterminer le coefficient 5 est peu précise pour les grands élancements[réf. nécessaire].
La ventilation de l'aval des cylindres en porte-à-faux

Les cylindres en porte-à-faux (de section circulaire, carrée, rectangulaire ou autres) présentés en travers du courant, bien que ne présentant à l'écoulement qu'une seule extrémité, sont également l'objet d'une ventilation de leur aval. Une description de l'écoulement sur de tels cylindres non-infinis (ou "finis", ou "en porte-à-faux") est proposée dans l'image ci-contre. La partie haute de l'écoulement (près de l'extrémité libre du cylindre) est évidemment comparable à l'écoulement sur les deux extrémités d'un cylindre fini.[réf. nécessaire]

Tetsushi Okamoto et Miki Yagita, par exemple, ont relevé les coefficients de pression à différentes hauteurs relatives sur des cylindres en porte à faux (en sous-critique au Reynolds 1,33 10^4). Le graphe ci-contre montre leurs mesures sur un cylindre en porte-à-faux d'élancement L/D = 9.
On remarque[réf. nécessaire] que, par rapport à la courbe rouge rappelant les autour du cylindre infini, la courbe blanche (qui montre les mesures de les plus proches de l'extrémité) est plus négative ; cette distribution de pression, après intégration, donne un très fort. Il en va de même de la courbe bleu très clair.
Très contre-intuitivement[réf. nécessaire], le local[n 6] de ces cylindres en porte-à-faux est nettement plus fort près de leur extrémité libre (il dépasse même les 1,2 du cylindre infini), comme le montre le premier graphe ci-dessous, pour divers élancements. Ce fait avait été observé en 1930 par Dryden et Hill[5], même si cet accroissement de la traînée locale près de l’extrémité n’augmente que de quelques pour cent le moment de traînée de tels cylindres par rapport à leur base (en comparaison avec le moment qu’on calculerait en supposant leur total réparti régulièrement en hauteur)[n 7]. Sur ce même graphe, on remarque à droite de chaque courbe la petite sinusoïde qui révèle l'existence d'un tourbillon en fer-à-cheval au pied du cylindre.
Les mesures d'Okamoto et Yagita[6] indiquent que si la couche limite qui s'est développée sur la plaque d'essais est peu épaisse (voir le dessin de gauche ci-dessous), on peut ajouter par la pensée au cylindre en porte-à-faux un cylindre symétrique (qu'on pourrait qualifier de cylindre miroir), ce qui reconstitue un cylindre à deux extrémités libres d'élancement double.
Le dernier graphe ci-dessous compare les quotients de traînées[n 8] de cylindres en porte-à-faux de différents élancements (en bleu) avec ceux des cylindres à deux extrémités libres (en rouge), l'abscisse des courbes des cylindres en porte-à-faux étant doublée : il apparaît que pour chaque élancement ces sont du même ordre. Ce fait autorise donc à extrapoler aux cylindres à deux extrémités libres les mesures de effectuées sur des cylindres en porte-à-faux[n 9].
-
 Crédit image:licence CC BY-SA 4.0 🛈Mode de contention d'un cylindre en soufflerie. Noter la position du cylindre (en porte-à-faux) très près du bord d'attaque de la plaque d'essais, ceci afin de minimiser la hauteur de la couche limite au pied du cylindre.
Crédit image:licence CC BY-SA 4.0 🛈Mode de contention d'un cylindre en soufflerie. Noter la position du cylindre (en porte-à-faux) très près du bord d'attaque de la plaque d'essais, ceci afin de minimiser la hauteur de la couche limite au pied du cylindre. -
 Crédit image:licence CC BY-SA 4.0 🛈local des cylindres finis à une extrémité libre d'Okamoto et Yagita.
Crédit image:licence CC BY-SA 4.0 🛈local des cylindres finis à une extrémité libre d'Okamoto et Yagita. -
 Crédit image:licence CC BY-SA 4.0 🛈Comparaison des locaux d'Okamoto et Yagita avec ceux obtenus par Goldstein pour le cylindre traversier infini.
Crédit image:licence CC BY-SA 4.0 🛈Comparaison des locaux d'Okamoto et Yagita avec ceux obtenus par Goldstein pour le cylindre traversier infini.
Notes
- Si on continue à faire décroître la longueur L à partir de la plaque carrée, le Cx frontal augmente à nouveau puisque, ce faisant, on forme une plaque rectangulaire de longueur H et de largeur L toujours exposée frontalement.
- On qualifie souvent les corps suscitant un écoulement 3D de "corps 3D", de même qu'on qualifie souvent les corps suscitant un écoulement 2D de "corps 2D".
- Cette méthode est également connue sous le nom de « Méthode d'Allen et Perkins ».
- ...portance linéaire calculée d'après le rapport des Barrowman
- En particulier, cette équation n'honore pas la marque à l'élancement 40 admise par Goldstein.
- Le local est celui d'une tranche de cylindre d'épaisseur dL (sur le modèle d'une tranche de saucisson) ; la surface de référence de ce local est donc la surface de la tranche telle que vue par l'écoulement, à savoir dL*D).
- Une intégration des locaux mesurés par Okamoto et Yagita montre (pour un cylindre d’élancement 12,5) une augmentation de seulement 4 % du moment dû à la traînée (par rapport à sa base) à cause de ce phénomène.
- Ce quotient de traînée est toujours défini comme le quotient du d'un cylindre de longueur finie sur le du cylindre infini
- Les mesures de traînée de cylindres en porte-à-faux sont plus faciles à effectuer, du fait des difficultés de contention des cylindres infinis
Références
- (en) T.A. Fox et G.S. West, « Fluid-Induced Loading of Cantilevered Circular Cylinders in a Low-Turbulence Uniform Flow. Part 1: Mean Loading with Aspect Ratios in the Range 4 to 30 », Journal of Fluids and Structures, vol. 7, no 1, 1993, pp. 1-14.
- (en) Sighard F. Hoerner, Fluid-Dynamic Drag, 1965, [lire en ligne] [PDF]
- (en) Sydney Goldstein, Modern Developments in fluid dynamics
- (en) Harry Julian Allen, Pressure Distribution and Some Effects of Viscosity on Slender Inclined Bodies of Revolution, NACA TN 204, 1950.
- (en) Hugh L. Dryden et George C. Hill, « Wind pressure on circular cylinders and chimneys », Bureau of Standards Journal of Research, vol. 5, no 3, pp. 653-693, 1930 [lire en ligne] [PDF].
- (en) Tetsushi Okamoto et Miki Yagita, « The Experimental Investigation on the Flow Past a Circular Cylinder of Finite Length Placed Normal to the Plane Surface in a Uniform Stream », Bulletin of JSME, vol. 16, no 95, mai 1973, pp. 805-814, [lire en ligne] [PDF].







