Pseudovecteur
En physique, un pseudovecteur ou vecteur axial est un vecteur de dimension 3 dont le sens dépend de l'orientation de l'espace. Plus précisément, l'inversion de l'orientation de l'espace se traduit par un changement de sens du pseudovecteur qui est donc changé en son opposé. On parle de pseudovecteurs par opposition aux vecteurs « ordinaires » (dits polaires) qui sont invariants par une telle inversion. Le produit vectoriel de deux vecteurs polaires est l'exemple type du pseudovecteur.
Pour satisfaire aux lois de la physique, on transforme un vecteur axial de la même manière qu'un vecteur polaire lors d'une isométrie directe (conservant les angles orientés comme une rotation) mais différemment lors d'une isométrie indirecte, par exemple une symétrie par rapport à un point ou par rapport à un plan[1] (voir la figure ci-dessous).
Les règles de calcul concernant les vecteurs axiaux sont ainsi différentes de celles des vecteurs polaires. Elles sont liées à celles des pseudo-vecteurs mathématiques (c'est-à-dire des bivecteurs), par exemple une 2-forme différentielle. En effet, une forme différentielle de degré 2 peut être représentée par une matrice antisymétrique de trois lignes et trois colonnes, possédant donc seulement trois composantes indépendantes auxquelles on peut faire correspondre un vecteur appelé vecteur dual. Si on considère les vecteurs duaux du bivecteur et de son transformé, ils se correspondent selon la loi des vecteurs axiaux (voir la figure ci-dessous et ici) et non selon la loi des vecteurs polaires[2].

Espace physique
En physique, les vecteurs ont d'abord été utilisés pour représenter des actions liées à des mouvements localement rectilignes. Ainsi la force qui s'exerce sur un objet selon un sens et une intensité peut être représentée par un vecteur polaire. Dans le cas d'un vecteur axial, l'action n'est plus dans la direction du vecteur mais dans une direction orthogonale au vecteur[4].
Le caractère polaire ou axial d'un vecteur est donc une notion physique qui n'a aucun équivalent mathématique[5]. Le qualificatif "axial" ou la notation avec une flèche incurvée[6] sont comme des "étiquettes" accolées au vecteur qui indiquent seulement comment on doit l'utiliser. Cela n'affecte aucunement son caractère vectoriel ; il faut donc rejeter l'appellation de " faux vecteur " dont est parfois affublé le vecteur axial.
Choix de l'orientation de l'espace

Un vecteur axial indique donc la direction de l'axe de rotation. Mais cela ne suffit pas : il faut aussi indiquer dans quel sens on tourne. Orienter l'espace, c'est indiquer quel est le sens positif de rotation. Pour cela, on utilise une convention[7] indépendante de tout repère : le sens positif de rotation autour de l'axe défini par le vecteur est obtenu en utilisant la règle du tire-bouchon de Maxwell. Ce sens positif de rotation est pour l'espace ce que le sens trigonométrique est pour le plan. D'ailleurs, si l'on considère le vecteur orthogonal au plan trigonométrique et orienté vers l'avant, cette convention redonne le sens trigonométrique. Comme c'est la main droite qui est utilisée (la main gauche donnerait le sens contraire), on dit que l'espace physique est orienté à droite. Cette convention est équivalente à la règle de la main droite qui permet de définir l'orientation d'un repère et par la suite l'orientation de l'espace. Le choix d'une orientation de l'espace est indispensable pour définir le produit vectoriel.
Si on avait choisi d'orienter l'espace physique à gauche, la même rotation aurait été représentée par le vecteur axial opposé. Par conséquent, dans les dessins, les vecteurs polaires resteraient inchangés alors que les vecteurs axiaux seraient remplacés par leur opposé (par contre, il n'y aurait aucune modification dans les formules). On exprime cela en disant qu'un vecteur axial dépend de l'orientation de l'espace[8].
Transformation physique


En mathématiques, un automorphisme de (c'est-à-dire un endomorphisme de inversible ) est souvent appelé une transformation de et l'image d'un élément (par cette transformation) est appelée son transformé. On se limitera ici aux transformations isométriques.
Vectoriellement, une isométrie directe est une rotation alors qu'une isométrie indirecte est, à une rotation près, une symétrie plane ou une inversion de l'espace[9]. Parmi les isométries indirectes, la première est simple à visualiser (comme l'image dans un miroir), la seconde appelée aussi symétrie P est simple à utiliser dans les formules.
Exemple
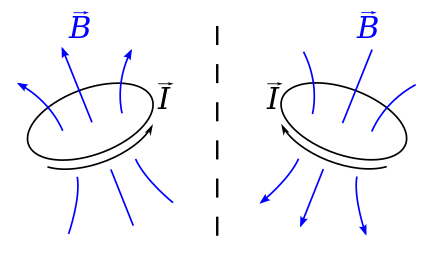
En physique, en association avec une transformation mathématique, on utilise aussi une autre transformation plus proche des concepts physiques. Par exemple dans le schéma ci-contre le vecteur représente le champ magnétique de la partie gauche. Son transformé physique est le vecteur qui représente le champ magnétique dans la partie droite c'est-à-dire (noté encore sur la figure). Par contre le transformé mathématique de est son symétrique par rapport au plan et il n'est pas égal à : c'est l'opposé. Cette ambiguïté concernant la transformation est à l'origine de la plupart des confusions. Par la suite, pour éviter ce problème, le transformé mathématique sera appelé « image » et le transformé physique sera simplement appelé « transformé ».
Cas général
Si l'on considère deux systèmes dont les éléments de position se correspondent à l'aide d'une isométrie (en supposant que ces systèmes restent isolés) on peut, pour chacun d'eux, les relier aux autres grandeurs du système[10] à l'aide des lois physiques qui constituent la théorie utilisée. Se pose alors la question de savoir comment se correspondent ces grandeurs et en particulier les vecteurs. Autrement dit, il reste à déterminer la transformation physique.
Si l'isométrie est directe (comme une rotation) tous les vecteurs se correspondent selon la transformation mathématique. Par contre si l'isométrie est indirecte (comme une symétrie plane ou centrale), les lois de la physique montrent que la transformation physique est identique à la transformation mathématique pour les vecteurs dits polaires, alors que c'est l'opposée de la transformation mathématique pour les vecteurs dits axiaux. Il faut bien remarquer que cette distinction « polaire/axial » ne concerne que la transformation physique et non la transformation mathématique[11].
Les vecteurs sont des objets mathématiques que la physique utilise comme bon lui semble. Pour rester en conformité avec les lois physiques en vigueur, la transformation physique est ainsi amenée à transformer les vecteurs d'une manière ou d'une autre selon leur caractère polaire ou axial. C'est une attitude pragmatique visant à combler une lacune d'un modèle mathématique simple, performant mais très légèrement insuffisant[12] ; les vecteurs polaires et axiaux ne sont pas de natures différentes (ce sont simplement des vecteurs) mais sont utilisés de manières différentes.
On utilise donc la règle pratique suivante :
L'ingérence de la physique dans les calculs mathématiques est assez inhabituelle (mais concerne néanmoins toutes les grandeurs axiales). D'ordinaire cette ingérence est inutile car le physicien choisit soigneusement l'outil mathématique dont les propriétés reflètent complètement celles du phénomène étudié (à tel point que souvent on commet l'abus de langage qui consiste à identifier le concept physique avec son modèle mathématique). Ce n'est manifestement pas le cas ici pour diverses raisons (notamment historiques et pratiques). Il existe d'autres modèles ne possédant pas cet inconvénient (somme toute assez mineur) mais ils sont plus complexes.
Utilisation du produit vectoriel
Pour être cohérent avec l'article pseudo-vecteur (mathématiques), on utilise les mêmes notations : "" pour le produit vectoriel, et "" pour le produit extérieur (usage exclusif).
Relation symboliques
Le produit vectoriel de deux vecteurs est un vecteur qui ne dépend pas du caractère polaire ou axial des vecteurs initiaux. Par contre le caractère polaire ou axial du produit est déterminé par les relations symboliques suivantes.
- polaire × polaire = axial
- axial × axial = axial
- polaire × axial = polaire
- axial × polaire = polaire
Le problème est donc scindé en deux parties indépendantes
- une partie purement mathématique qui consiste à calculer le produit vectoriel,
- une partie purement physique qui consiste à affecter à ce produit le caractère polaire ou axial.
Le rotationnel pouvant s'écrire comme un produit vectoriel, tout vecteur axial est un produit vectoriel ou une somme de produits vectoriels (la réciproque étant fausse).
Exemples
En physique, on utilise le plus souvent des champs de vecteurs même si le mot « champ » est souvent omis.
- Vecteurs polaires
- vecteur position et ses dérivées (vecteur vitesse et vecteur accélération),
- champ électrique ,
- potentiel vecteur .
- Vecteur axial
- champ magnétique . Le caractère axial de apparaît aussi dans la loi de Biot et Savart .
- moment magnétique
- moment cinétique
- moment d'une force :
- vecteur tourbillon .
- Composition
- le produit vectoriel du vecteur vitesse angulaire et du vecteur rayon jusqu'au centre de rotation donne la vitesse du point considéré : c'est la formule de Varignon.
- le produit vectoriel du vecteur accélération angulaire et du rayon vecteur donne l'accélération du point considéré.
- Torseurs
- dans le cas d'un torseur cinétique, dynamique ou statique, la résultante est un vecteur polaire et le moment est un vecteur axial.
- dans le cas d'un torseur cinématique, la résultante est un vecteur axial et le moment est un vecteur polaire.
Utilisation du produit scalaire
Scalaire axial
Cette dénomination est utilisé, par exemple, par Sivardière, p.1244.
« Tant que la symétrie géométrique ordinaire est seule considérée, on est amené à classer les grandeurs physiques en deux catégories : les grandeurs polaires, dont le signe ne dépend pas de la convention d’orientation de l’espace, et les grandeurs axiales, dont le signe en dépend »[13]. Insistons sur le fait qu'une grandeur axiale dépend de l'orientation de l'espace (comme il est dit ci-dessus) mais qu'elle est complètement indépendante de tout repère et donc a fortiori de son orientation ; c'est par conséquent un tenseur et non un pseudo-tenseur.
Le produit scalaire de deux vecteurs est un scalaire qui ne dépend pas du caractère polaire ou axial des vecteurs initiaux. Par contre le caractère axial ou non du produit est déterminé de la manière suivante :
- si l'un des vecteurs est polaire et l'autre axial, alors le produit est un scalaire axial ;
- sinon, le produit est un scalaire "ordinaire".
De même qu'un vecteur axial est appelé "pseudovecteur" alors que ce n'est ni un pseudo-vecteur au sens mathématique ni un pseudo-tenseur d'ordre 1 (voir Pseudo-vecteur (homonymie)), un scalaire axial est le plus souvent appelé "pseudoscalaire" alors que ce n'est ni un pseudo-scalaire au sens mathématique (voir, par exemple, ici) ni un pseudo-tenseur d'ordre 0.
Transformation
Tout scalaire axial est égal au produit scalaire de deux vecteurs, l'un axial et l'autre polaire (ou à la somme de tels produits). Par conséquent, lors d'une isométrie indirecte, le scalaire axial doit être changé en son opposé. De nouveau, le scalaire ne fait pas cela "de lui-même" : c'est le physicien qui effectue cette opération pour être en conformité avec les lois physiques de la théorie utilisé. Cela est valable en fait, pour toute grandeur axiale.
Produit mixte
Soit trois vecteurs polaires. Le produit mixte de ces trois vecteurs est ; d'après ce qui précède, c'est un scalaire axial. En fait, le caractère axial peut être obtenu plus directement car où est le tenseur de Levi-Civita qui dépend, par définition, de l'orientation.
Si est une isométrie, alors . On retrouve le résultat précédent.
Vecteur axial vs bivecteur
Ce paragraphe fait la liaison entre cet article et l'article Pseudo-vecteur (mathématiques) ; une connaissance même superficielle de ce dernier n'est pas nécessaire mais est souhaitable.
Le vecteur axial est le vecteur dual de la 2-forme différentielle (qui est un bivecteur). Plus généralement, en physique tout vecteur axial est le vecteur dual d'un bivecteur[14]. Tous deux peuvent représenter la grandeur physique concernée et, a priori, aucun n'est plus légitime que l'autre. Les lois physiques montrent que, lors d'une isométrie, c'est le bivecteur qui doit être transformé (mathématiquement), le vecteur dual étant récupéré après coup à partir de l'image du bivecteur (comme sur le schéma ici) ; si on transforme (mathématiquement) le vecteur dual, cela ne convient pas. De ce point de vue, il semblerait donc que le bivecteur soit le seul légitime. Mais d'un autre point de vue, le vecteur axial est beaucoup plus pratique d'emploi. Finalement, accoler l'adjectif "axial" au vecteur dual apparaît comme un moyen astucieux de court-circuiter le bivecteur, car la transformation physique est une technique pratique toute simple qui permet de profiter du meilleur des deux mondes.
Confusion entre bivecteur et vecteur axial
En dimension 3 (ce ne serait plus vrai en relativité par exemple), un bivecteur est un pseudo-vecteur au sens mathématiques. Il faut éviter la confusion "pseudo-vecteur alias bivecteur" avec "pseudovecteur alias vecteur axial" (voir Pseudo-vecteur (homonymie)) car, même s'ils sont duaux l'un de l'autre, ils ont des propriétés bien distinctes[15].
Dans la pratique, les coordonnées du produit vectoriel ne sont calculées que dans une base orthonormale directe. Dans ce cas, en modifiant de façon ad hoc[16] la base canonique des bivecteurs, on obtient l'égalité des coordonnées du produit extérieur et du produit vectoriel (c'est-à-dire d'un bivecteur et de son vecteur dual) et cette égalité est conservée lors d'un changement de base orthonormale directe ; la confusion ne mène alors à aucune erreur et est malheureusement assez répandue. Il est nécessaire de la disqualifier, car dès que l'on fait un peu de théorie et que l'on s'écarte de ces conditions particulières, rien ne va plus.
La distinction polaire/axiale est-elle nécessaire ?
Elle n'est pas nécessaire mais s'avère très utile en pratique. La représentation vectorielle de l'électromagnétisme est un modèle élémentaire, facilement accessible mais ce n'est qu'un modèle parmi d'autres. Dans le formalisme de la relativité, le champ électromagnétique est représenté par un tenseur antisymétrique (en dimension 4). Dans ce cadre, les vecteurs et sont définis pour faire le lien avec la représentation vectorielle mais ne sont pas utilisés comme tels. Il en est de même dans la représentation (moins connue) de l'Algèbre géométrique. Dans ces deux derniers modèles, la distinction polaire/axial est inutile.
Dire que « est le champ magnétique » ne pose pas de problème si l'on est conscient que c'est un abus de langage. Sinon, cela conduit à prêter au vecteur des propriétés qu'aucun objet mathématique (ou réel) ne peut posséder[17].
Champ de vecteurs
Ce qui précède peut se généraliser aux champs vectoriels. Les exemples physiques donnés précédemment sont en fait des champs de vecteurs (pour alléger l'expression, on dit le plus souvent « vecteur » au lieu de « champ de vecteurs »). La distinction « polaire/axial » est particulièrement importante dans l'analyse des propriétés de symétrie des champs de vecteurs (cf. Principe de Curie). Ainsi, le champ électrique (vecteur polaire) possède les mêmes symétries que ses sources : un plan de symétrie des charges est plan de symétrie de . Par contre, le champ magnétique (vecteur axial) inverse ces propriétés : un plan de symétrie des courants est plan d'antisymétrie de [18]. Mettre ces plans en évidence (lorsqu'ils existent) permet de simplifier les calculs.
Nous supposons connus les trois opérateurs différentiels gradient, divergence et rotationnel que de nombreuses formules relient entre eux (cf. ici) ; on se contente de mettre en évidence leur caractère axial ou polaire. Les expressions sont données à l'aide des coordonnées locales, en se limitant au cas le plus élémentaire : coordonnées cartésiennes dans un repère orthonormal direct[19]. Les relations de ce type les plus générales utilisent la notion de dérivée covariante et conduisent aux mêmes conclusions.
Les exemples sont issus de l'électromagnétisme et plus précisément des équations de Maxwell.
Opérateur nabla
On note l'opérateur de dérivation et on définit l'opérateur nabla comme ayant les " coordonnées " symboliques . Son intervention dans les produits scalaires, vectoriel ou extérieur se fait simplement en utilisant ses " coordonnées " comme si c'étaient les coordonnées covariantes d'un vecteur.
Gradient
Soit une fonction à valeurs réelles. Le vecteur a pour coordonnées . Ce sont celles du vecteur gradient et on note . Le gradient d'une fonction scalaire est un champ de vecteurs polaires. Exemple
Divergence
Soit un vecteur de coordonnées . Le scalaire est égal à la divergence de et on note . La divergence d'un champ de vecteurs polaires est une fonction scalaire. Exemple
Rotationnel
Soit un covecteur de coordonnées . Le pseudo-vecteur a pour coordonnées et son vecteur dual a pour coordonnées où est le symbole de Levi-Civita. Ce sont les coordonnées du rotationnel, et on note . Le rotationnel d'un champ de vecteurs est un champ de vecteurs. Plus précisément :
- Le rotationnel d'un vecteur polaire est un vecteur axial. Exemple .
- Le rotationnel d'un vecteur axial est un vecteur polaire. Exemple
Notes
- ↑ Taillet, p. 449-450.
- ↑ « On associe donc un vecteur à ce tenseur, et on ne fait intervenir explicitement dans les formules que ce vecteur« adjoint ». Ceci entraîne des difficultés, du fait que le vecteur adjoint ne se transforme pas comme un vecteur mais comme le tenseur du second ordre qu’il représente : d’où la nécessité de dénominations et de notations particulières (vecteur « axial », ), et celle de bien distinguer la nature des êtres dont les constituants sont des vecteurs et des pseudovecteurs. »Vogel, p.86.
- ↑ C'est le physicien qui le transforme différemment et non le vecteur qui se transforme de lui même de façon différente.
- ↑ « La direction et la grandeur d'une quantité peuvent dépendre d'une action ou d'un effet qui se produit entièrement suivant une certaine ligne, ou bien elles peuvent dépendre de quelque élément qui est de la nature d'une rotation autour de cette ligne prise comme axe. » Maxwell, §15 p.13.
- ↑ « La plupart des physiciens utilise, concurremment avec les tenseurs vrais, des êtres tels que les vecteurs axiaux, les densités et les capacités tensorielles, dont les lois de transformation sont différentes, et qui ne se rencontrent pas, en général, dans les traités dus à des mathématiciens. »Vogel, résumé.
- ↑ Pour signaler que l'on affaire à un vecteur axial on peut aussi le noter avec une flèche courbée (dans le sens antihoraire qui symbolise la rotation). Exemple : pour le vecteur axial vitesse de rotation.
- ↑ Cette convention pour orienter l'espace et aussi appelée convention d'orientation des angles. Sivardière, p.1240.
- ↑ Au lieu de "l'orientation de l'espace", on trouve souvent (comme chez Robert, p.326 par exemple) "l'orientation du trièdre de référence". Comme cette expression est ambigüe (voir ici) on ne l'utilisera pas.
- ↑ Une transformation active qui à tout vecteur fait correspondre son opposé. A ne pas confondre avec la transformation passive (un changement de base) qui fait passer de la base à la base .
- ↑ « Un système physique isolé quelconque fait appel pour sa description non seulement à des coordonnées de position mais à des grandeurs moins immédiatement liées à des positions. Ces grandeurs sont usuellement classées dans le cadre des entités tensorielles en grandeurs scalaires (masse, charge électrique, masse magnétique, énergie ) et vectorielles (vitesse, accélération, champ électrique, champ magnétique, force, moment cinétique, couple ), en nous désintéressant pour la simplicité de l'exposé, des grandeurs tensorielles d'ordre plus élevées. » Berthelot, p.49.
- ↑ C'est la confusion entre ces deux transformations (physique et mathématique) qui conduit à qualifier un vecteur axial de " faux " vecteur croyant ainsi expliquer l'origine du mot « pseudo-vecteur », le préfixe pseudo étant alors pris dans son sens étymologique (c'est-à-dire " faux ").
- ↑ « Dans la représentation vectorielle standard [de l'électromagnétisme], le vecteur E est dit polaire alors que le vecteur B est dit axial, les deux types de vecteurs étant distingués par une différence de signe sous une inversion d'espace. L'algèbre géométrique (AG) met en évidence le fait qu'un vecteur axial n'est qu'un bivecteur représenté par son dual, et qu'ainsi le champ magnétique est pleinement représenté par le bivecteur complet iB, plutôt que par B tout seul. Par conséquent, AG rend inutile l'embarrassante distinction entre les vecteurs polaires et axiaux. »
« In standard vector algebra E is said to be a polar vector while B is an axial vector, the two kinds of vector being distinguished by a difference in sign under space inversion. GA reveals that an axial vector is just a bivector represented by its dual, so the magnetic field in (31) is fully represented by the complete bivector iB, rather than B alone. Thus GA makes the awkward distinction between polar and axial vectors unnecessary ». Hestenes, p.16. - ↑ Sivardière, p.10.
- ↑ Voir, par exemple, ici.
- ↑ « Les termes vecteur axial et pseudo-vecteur sont souvent considérés comme synonymes, mais il est plutôt utile de pouvoir distinguer un bivecteur de son dual », « The terms axial vector and pseudovector are often treated as synonymous, but it is quite useful to be able to distinguish a bivector from its dual. » Baylis, p.234 (footnote).
- ↑ c'est-à-dire en prenant à la place de .
- ↑ Le vecteur se comporterait comme Edward James dans le tableau La Reproduction interdite de René Magritte (illustration disponible dans l'article en anglais).
- ↑ Attention à ne pas dire (par identification du vecteur avec le concept physique) « plan d'antisymétrie du champ magnétique » car le champ magnétique étant un phénomène physique, cela violerait le principe de Curie.
- ↑ Dans un repère orthonormal, les coordonnées covariantes et contravariantes sont identiques. Cela nous permettra de mettre à notre convenance les indices en position covariante ou contravariante afin de pouvoir utiliser la convention de sommation d'Einstein.
Références
Bibliographie
- (en) William E Baylis, Theoretical methods in the physical sciences: an introduction to problem solving using Maple V, Birkhäuser, (ISBN 0-8176-3715-X)
- André Berthelot, Les développements récents relatifs à la symétrie droite-gauche en physique, Paris, J.-B Baillière et fils, coll. « L'information scientifique » (no 2), , p. 47-62
- (en) David Hestenes, Oersted Medal Lecture 2002: Reforming the Mathematical Language of Physicsréférence
- James Clerc Maxwell, Traité d'électricité et de magnétisme, t. 1, Paris, Gauthiers-Villars, 1885 (traduction française du traité original de 1873)
- Jean-Louis Basdevant, Xavier Bataille, Philippe Fleury, Patrick Kohl et Jérôme Robert (coordinateur), Dictionnaire de physique et de chimie, Paris, Nathan,
- Jean Sivardière, Les grandeurs physiques axiales, coll. « Bulletin de l'Union de Physiciens » (no 709), , p. 1239-1261
- Jean Sivardière, L'antisymétrie en physique élémentaire, vol. 87, coll. « Bulletin de l'Union de Physiciens », , p. 7-23
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, De Boeck, , 2e éd.
- Théodore Vogel, Sur l’utilisation des pseudo-tenseurs en physique, t. 18, n°2, coll. « Le journal de Physique et Le Radium, 10.1051/jphysrad:0195700180208100 », (HAL jpa-00235630), p. 81-84
Voir aussi
Articles connexes
- Matrice antisymétrique
- Pseudoscalaire, Scalaire
- Covecteur
 , Espace dual
, Espace dual - Tenseur
- Analyse vectorielle
- Orientation
- Grandeur d'orientation
Liens externes
- www.isima.fr/~leborgne/IsimathMeca/Produitvectoriel.pdf. "Produit vectoriel, pseudo-produit vectoriel, et endomorphismes antisymétriques". 9 pages.
















![{\displaystyle [x_{1},x_{2},x_{3}]=(x_{1}\times x_{2})\centerdot x_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b52b34bb83d5b5a273c6674052a1e8d691b6267)
![{\displaystyle [x_{1},x_{2},x_{3}]=\eta (x_{1},x_{2},x_{3})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e38d2b5dc5cdee9d181002cf368e9c1d0045126)


![{\displaystyle [h(x_{1}),h(x_{2}),h(x_{3})]=\det(h)\,[x_{1},x_{2},x_{3}]=\pm [x_{1},x_{2},x_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef83fab8a68244fddbed3ad3ccc91066230ae6d)

































