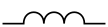Introduction à l'électromagnétisme
L'électromagnétisme est une branche de la physique qui étudie l'interaction électromagnétique, l'une des quatre forces fondamentales de la nature. Au début, l'électricité et le magnétisme étaient étudiés séparément et considérés comme des phénomènes distincts, avec leurs propres équations. Dans les années 1820, Hans Christian Ørsted découvrit que les deux phénomènes étaient liés : un courant électrique donne naissance au magnétisme et peut mettre en mouvement l'aiguille d'une boussole. Michael Faraday découvrit ensuite que l'inverse était également possible : le magnétisme peut induire des courants électriques. En 1865, James Clerk Maxwell rassembla le tout dans une théorie unifiée de l'électromagnétisme. Les équations de Maxwell indiquent en outre que les ondes électromagnétiques sont bien réelles. Des expériences de Heinrich Hertz l'ont ensuite confirmé, rendant possible la transmission par ondes radio. Maxwell avait également postulé, à juste titre, que la lumière était une forme d'onde électromagnétique, faisant ainsi de toute l'optique une branche de l'électromagnétisme. Les ondes radio ne diffèrent de la lumière que par le fait que leur longueur d'onde est beaucoup plus longue. Albert Einstein a finalement montré que le champ magnétique résultait de l'effet relativiste du champ électrique et que le magnétisme n'était donc qu'un effet secondaire de l'électricité qui n'apparaît que lorsque les charges sont en mouvement. Le traitement théorique moderne de l'électromagnétisme est celui d'un champ quantique en électrodynamique quantique.
Dans de nombreuses situations rencontrées en génie électrique, il n'est pas nécessaire d'utiliser la théorie quantique pour obtenir des résultats satisfaisants. La physique classique est une approximation suffisamment précise dans la plupart des situations impliquant des objets macroscopiques (voir l'article longueur électrique). La théorie quantique n'est nécessaire, à quelques exceptions près, qu'à l'échelle atomique et un traitement classique plus simple peut être appliqué dans la plupart des autres cas. Des simplifications supplémentaires sont également possibles dans quelques situations limitées. L'électrostatique ne traite que des charges électriques stationnaires, de sorte que les champs magnétiques n'apparaissent pas et n'ont pas besoin d'être pris en compte. Les aimants permanents peuvent être décrits sans faire référence à l'électricité ou à l'électromagnétisme. La théorie des circuits (ou réseaux) électriques traite de réseaux au sein desquels les champs sont largement confinés autour des conducteurs transportant le courant. Dans de tels circuits, même les équations de Maxwell peuvent être ignorées et des formulations plus simples peuvent être utilisées. D'un autre côté, un traitement quantique de l'électromagnétisme est important dans le domaine de la chimie. Les réactions chimiques et les liaisons chimiques sont le résultat d'interactions quantiques entre les électrons localisés en périphérie des atomes. Des considérations quantiques sont également nécessaires pour expliquer le comportement de nombreux dispositifs électroniques. C'est le cas, par exemple, de la diode à effet tunnel.
Charge électrique

L'électromagnétisme est l'une des quatre forces fondamentales de la nature, les trois autres étant la gravité, la force nucléaire forte et la force nucléaire faible. Alors que la gravité agit sur tout ce qui a une masse, l'électromagnétisme agit sur tout ce qui a une charge électrique. De plus, de la même façon qu'il y a une loi de conservation de la masse, selon laquelle aucune masse ne peut être créée ni détruite, il y a également une loi de conservation de la charge électrique, selon laquelle la charge totale dans un système fermé (un système pour lequel aucune charge ne sort ni n'entre) reste constante[1]. La loi fondamentale qui décrit la force gravitationnelle sur un objet massif en physique classique est la loi universelle de la gravitation de Newton. D'une manière analogue, la loi de Coulomb est la loi fondamentale qui décrit la force que les objets chargés exercent les uns sur les autres. Elle est donnée par la formule[2]:6 où est la constante de Coulomb, et sont les valeurs des deux charges, est la distance qui les sépare, et est le vecteur unitaire de la direction depuis la charge qui exerce la force vers celle qui la subit. L'intensité de la force s'exprime alors par Les charges électriques pouvant avoir soit un signe positif, soit un signe négatif, cette formule décrit le fait que des charges ayant le même signe se repoussent alors que des charges de signes opposés s'attirent. Elle montre également que plus les charges des particules sont grandes, plus la force qu'elles exercent les unes sur les autres est élevée. La loi est également une loi en carré inverse, ce qui signifie que lorsque la distance entre deux particules est doublée, la force exercée sur elles est réduite d'un facteur quatre[3].
Champs électriques et magnétiques

En physique, les champs sont des entités qui interagissent avec la matière. On les décrit mathématiquement en leur attribuant une valeur en chaque point de l'espace et du temps. Les champs vectoriels sont des champs auxquels on attribue à la fois une valeur numérique et une direction en chaque point de l'espace et du temps. Les charges électriques produisent un champ vectoriel appelé champ électrique. La valeur numérique du champ électrique, également appelée intensité du champ électrique, détermine l'intensité de la force électrique qu'une particule chargée ressentira si elle est placée dans le champ. La direction du champ détermine la direction de la force. Par convention, la direction du champ électrique est la même que la direction de la force agissant sur des charges positives, et elle est opposée à la direction de la force agissant sur des charges négatives[4],[5]. Comme les charges positives sont repoussées par d'autres charges positives et attirées par les charges négatives, cela signifie que les flèches symbolisant les lignes de champ électrique s'éloignent des charges positives et s'orientent vers les charges négatives. Ces propriétés du champ électrique sont résumées dans l'expression suivante de la force électrique sur une charge, écrite en termes de champ électrique[2]:6 :
où est la force agissant sur la charge placée en un point de l'espace où règne un champ électrique [5],[1].
En plus de produire un champ électrique, les particules chargées, lorsqu'elles sont en mouvement, produisent un champ magnétique. D'autres charges électriques lorsqu'elles sont en mouvement (ainsi que les aimants permanents) ressentiront une force magnétique si elles traversent ce champ magnétique[6]. La direction de cette force est perpendiculaire à la fois à la direction du mouvement de la charge qui subit la force et à la direction des lignes de champ magnétique. Cette direction est donnée par la règle de la main droite. La force est donnée par l'équation[2]:45 où la charge q a une vitesse et se trouve en un lieu où règne le champ magnétique . Le symbole représente le produit vectoriel entre et . L'intensité de la force est donnée par où est l'angle que fait la direction du champ (le vecteur ) par rapport à la direction du mouvement de la charge (le vecteur )[7].
La combinaison des forces électriques et des forces magnétiques qui agissent sur une particule chargée s'appelle la force de Lorentz[7],[1]. L'électromagnétisme classique est entièrement décrit par la force de Lorentz, aux côtés d'un ensemble de quatre équations appelées les équations de Maxwell. La première de ces équations est connue sous le nom de théorème de Gauss. Elle décrit le champ électrique produit par des particules chargées et par des distributions de charge. Selon le théorème de Gauss, le flux de champ électrique qui sort de toute surface fermée est proportionnel à la quantité de charge qui est situé à l'intérieur de cette surface[8],[9]. Cela signifie que plus la charge est élevée, plus le champ électrique généré est important. Le théorème de Gauss a aussi d'autres implications importantes. Par exemple, il signifie que s'il n'y a pas de charge enfermée à l'intérieur d'une surface, alors soit il n'y a pas de champ électrique du tout, soit, s'il y a une charge à l'extérieur de la surface, le champ électrique que cette charge engendre est tel que le flux de champ électrique entrant par la surface doit s'annuler exactement avec le flux ressortant de l'autre côté[10].
La seconde équation de Maxwell est l'équivalent de la première pour le cas du magnétisme. Elle décrit que le flux de champ magnétique à travers une surface fermée est toujours nul. Cela signifie que s'il y a un champ magnétique, le flux entrant par la surface fermée s'annulera toujours avec le flux sortant de cette même surface, ce qui a pour conséquence que tout flux magnétique sortant d'une surface fermée doit y retourner. Ainsi, un pôle magnétique positifs et un pôle magnétique négatifs doivent toujours se regrouper en un dipôle magnétique et ne peuvent jamais être séparés en monopôles magnétiques[1]. Cela contraste avec les charges électriques qui peuvent exister sous forme de charges positives et de charges négatives séparées.

La troisième équation de Maxwell s'appelle le théorème d'Ampère. Elle stipule qu'un champ magnétique peut être généré par un courant électrique[11]. La direction du champ magnétique est donnée par la règle de la main droite. Si le fil est droit, le champ magnétique s'enroule autour de lui comme les doigts lorsque l'on ferme le poing de la main droite avec le pouce indiquant la direction du courant. Si le fil est enroulé pour former une bobine, le champ magnétique à l'intérieur de la bobine pointe dans la direction du pouce tendu lorsque les doigts se referment dans le sens du courant[12]. Lorsque des courants électriques sont utilisés pour produire un aimant de cette manière, le dispositif est appelé un électroaimant. Les électroaimants utilisent souvent un fil enroulé en solénoïde autour d'un noyau de fer qui renforce le champ magnétique produit parce que le noyau de fer se magnétise[13],[14]. Une extension, dite de Maxwell, de cette loi stipule qu'un champ électrique variant dans le temps peut également générer un champ magnétique[1].
De même, la loi d'induction de Lenz-Faraday stipule qu'un champ magnétique peut produire un courant électrique. Par exemple, un aimant que l'on fait se déplacer d'avant en arrière le long de l'axe d'une bobine de fils produit un courant électrique dans la bobine. La force électromotrice produite est proportionnelle à l'intensité de l'aimant, au nombre de spires de la bobine et à la vitesse à laquelle l'aimant est déplacé dans la bobine. Ce principe est essentiel pour les transformateurs qui sont utilisés pour transformer des courants de tension élevée en courants de tension plus faible, et vice versa. Ils sont nécessaires pour convertir l'électricité produit dans les centrales à haute tension en électricité basse tension qui peut être utilisée en toute sécurité dans les maisons. La formulation de Maxwell de la loi est donnée par la quatrième équation de Maxwell, l'équation de Maxwell-Faraday. Elle stipule qu'un champ magnétique variant dans le temps produit un champ électrique.

Les quatre équations de Maxwell sont en fait les versions locales des lois de l'électromagnétisme. Ce sont les quatre équations aux dérivées partielles suivantes[2] : où et sont respectivement les opérateurs divergence[note 1] et rotationnel[note 2], est la densité de charge, est le vecteur densité de courant, et sont respectivement la permittivité diélectrique du vide et la perméabilité magnétique du vide. Le symbole représente la dérivée partielle par rapport au temps.
Ensemble, les quatre équations de Maxwell fournissent une seule et même théorie uniforme pour les champs électriques et pour les champs magnétiques. Le travail de Maxwell qui conduisit à la mise en place de cette théorie a été qualifié de « deuxième grande unification de la physique », après la première qu'avait été la loi de la gravitation universelle de Newton[15]. La solution des équations de Maxwell dans le vide (où il n'y a ni charges ni courants électriques) conduit à l'équation des ondes, qui correspond aux ondes électromagnétiques (ayant une composante électrique et une composante magnétique) se déplaçant à la vitesse de la lumière[16]. Étant arrivé à la conclusion que les solutions de l'équation des ondes avaient une vitesse de propagation exactement égale à celle de la lumière, Maxwell avait émis l'hypothèse que la lumière était une forme de rayonnement électromagnétique et avait postulé que d'autres rayonnements électromagnétiques pourraient exister avec des longueurs d'onde différentes[17]. L'existence du rayonnement électromagnétique a été prouvée par Heinrich Hertz dans une série d'expériences entre 1886 et 1889 au cours desquelles il découvrit l'existence des ondes radio. Le spectre électromagnétique complet (par ordre de fréquence croissante) comprend les ondes radio, les micro-ondes, le rayonnement infrarouge, la lumière visible, le rayonnement ultraviolet, les rayons X et les rayons gamma[18].
Une autre unification de l'électromagnétisme c'est produite avec la théorie de la relativité restreinte d'Albert Einstein. Selon la relativité restreinte, des observateurs se déplaçant à des vitesses différentes les uns par rapport aux autres occupent des référentiels d'observation différents. Pour un observateur en mouvement par rapport à un autre observateur, la mesure de la longueur d'un objet se déplaçant avec la même vitesse qu'un second observateur est plus petite que la mesure que ferait ce second observateur, pour qui l'objet apparaît immobile. On parle de contraction des longueurs. Par conséquent, lorsqu'un électron se déplace dans un fil neutre, les électrons circulant dans le fil à la même vitesse que lui apparaissent comme étant immobiles. Mais les charges positives se déplacent par rapport à lui, et elles forment donc un ensemble qui apparaît contracté de son point de vue. Selon le référentiel que l'on utilise, la perception des champs électrique et magnétique sera différente pour cet électron. Dans le référentiel du laboratoire, l'électron se déplace et il ressent donc une force magnétique produite par le courant circulant dans le fil, mais puisque le fil est neutre, il ne ressent aucune force électrique. Dans le référentiel de l'électron, les charges positives semblent être plus denses que les charges négatives des électrons, du fait de la contraction discutée ci-dessus. Le fil apparaît donc chargé positivement pour l'électron. Par conséquent, dans le référentiel de l'électron, ce dernier ne ressent aucune force magnétique (car il ne se déplace pas dans son propre référentiel), mais il ressent une force électrique due au fil chargé positivement. Ce résultat de la relativité montre que les champs magnétiques ne sont que des champs électriques vus dans un référentiel différent (et vice versa). Les deux ne sont donc que des manifestations différentes du même phénomène sous-jacent, le champ électromagnétique[1],[19],[20].
Conducteurs, isolants et circuits
Conducteurs


Un conducteur est un matériau dans lequel certains électrons peuvent circuler librement. Les conducteurs les plus efficaces sont généralement les métaux qui peuvent être décrits assez précisément par le modèle des électrons libres dans lequel les électrons se délocalisent des noyaux atomiques, laissant des ions positifs entourés d'une mer d'électrons libres[21]. Des exemples de bons conducteurs sont le cuivre, l'aluminium et l'argent. Les fils électriques sont souvent en cuivre[22].
Les principales propriétés des conducteurs parfaits sont[2]:33,[1] :
- Le champ électrique est nul à l'intérieur du conducteur. Comme les charges sont libres de se déplacer dans le conducteur, lorsqu'elles sont perturbées par un champ électrique extérieur, elles se réarrangent de telle sorte que le champ produit par leur configuration annule exactement le champ électrique extérieur à l'intérieur du conducteur.
- Le potentiel électrique est le même partout à l'intérieur du conducteur et sur sa surface. Cela découle de la première propriété car le champ étant nul partout à l'intérieur du conducteur, le potentiel est constant à l'intérieur du conducteur, puisque le champ est le gradient (la dérivée par rapport à l'espace) du potentiel.
- Le fait que le champ électrique soit nul à l’intérieur du conducteur implique également que la densité de charge volumique est nulle à l'intérieur du conducteur. Les charges en excès, s'il y en a, se répartissent sur la surface du conducteur.
- Sur la surface d'un conducteur, le champ électrique est perpendiculaire à la surface. Si ce n'était pas le cas, le champ aurait une composante non nulle à la surface du conducteur, ce qui entraînerait le déplacement des charges dans le conducteur jusqu'à ce que cette composante du champ devienne nulle.
- Le flux électrique net à travers une surface est proportionnel à la charge enfermée par la surface. Il s'agit d'une reformulation du théorème de Gauss.
Dans la plupart des matériaux, les électrons sont liés aux noyaux atomiques et ne sont donc pas entièrement libres de se déplacer, bien que l'énergie nécessaire pour les libérer soit faible. Dans ces matériaux, que l'on appelle des semi-conducteurs, la conductivité est faible à basse température, mais à mesure que la température augmente, les électrons gagnent plus d'énergie thermique et peuvent se libérer, ce qui augmente la conductivité[23]. Le silicium est un exemple de semi-conducteur qui peut être utilisé pour créer des panneaux solaires. Ces derniers deviennent plus conducteurs à mesure qu'ils reçoivent de l'énergie lumineuse émise par le soleil[24].
Les matériaux supraconducteurs présentent peu, voire pas du tout, de résistance au courant électrique lorsqu'ils sont refroidis en dessous d'une certaine température critique. La supraconductivité ne peut être expliquée que par le principe d'exclusion de Pauli de la mécanique quantique. Ce dernier stipule que deux fermions (les électrons sont des fermions) ne peuvent occuper exactement le même état quantique. Dans les supraconducteurs, lorsque la température descend en dessous d'une certaine valeur, les électrons forment des paires de Cooper, qui constituent des bosons et qui ne satisfont donc pas au principe d'exclusion de Pauli. Ceci signifie que tous les électrons peuvent se retrouver au même niveau d'énergie et se déplacer ensemble uniformément dans un courant[25].
Isolants

Teresa Martín Blas y Ana Serrano Fernández.
EUIT Forestal - Universidad Politécnica de Madrid - EspañaLes isolants sont des matériaux très résistants au courant électrique et sont donc souvent utilisés pour recouvrir les fils conducteurs pour des raisons de sécurité. Dans un matériau isolant, les électrons sont fortement liés aux noyaux atomiques et l'énergie nécessaire pour les libérer est très élevée, ils ne sont donc pas libres de se déplacer et résistent au mouvement que leur impose un champ électrique externe[26]. Cependant, certains isolants, appelés diélectriques, peuvent être polarisés sous l'influence d'un champ électrique externe. Les charges positives se déplacent légèrement dans la direction du champ, alors que les charges négatives se déplacent légèrement dans la direction opposée, tout en restant liées au réseau cristallin, de sorte qu'il se forme localement des dipôles minuscules (à l'échelle atomique) constitués d'un côté positif et d'un côté négatif[27]. Les diélectriques sont utilisés dans les condensateurs pour leur permettre de stocker plus d'énergie potentielle électrique dans le champ électrique régnant entre les armatures du condensateur[28].
Condensateurs


Un condensateur est un composant électronique qui emmagasine de l'énergie potentielle sous la forme d'un champ électrique entre deux armatures conductrices séparées par un matériau diélectrique. Les deux armatures collectent des charges électriques de signe opposés, créant un champ électrique entre les deux. Si les deux armatures ont une densité de charge égale à et respectivement, A étant la surface des armatures, alors il règne un champ électrique entre elles. La différence de potentiel entre deux armatures parallèles peut se calculer mathématiquement par[29] où d est la distance séparant les deux armatures et est la permittivité diélectrique du vide. L'aptitude d'un condensateur à emmagasiner de l'énergie potentielle électrique est mesurée par sa capacité qui est définie par . Dans le cas d'un condensateur à armatures parallèles, on obtient donc[29] Si un diélectrique est placé entre les armatures, la permittivité du vide est multipliée par la permittivité relative du diélectrique, qui est supérieur à 1, augmentant la capacité du condensateur[28]. L'énergie maximale pouvant être emmagasinée par un condensateur est proportionnelle à sa capacité et au carré de la différence de potentiel entre les deux armatures[29] :
Bobines d'inductance
Une bobine d'inductance est un composant électronique qui emmagasine de l'énergie sous la forme d'un champ magnétique à l'intérieur d'une bobine de fil. Une bobine conductrice parcourue par un courant électrique induit un champ magnétique qui peut être déterminé par le théorème d'Ampère. La bobine est caractérisée par son inductance, définie par , où est le flux du champ magnétique à travers la section entourée par la bobine. Plus le courant est important, plus l'énergie emmagasinée dans le champ magnétique est importante et plus l'inductance est faible. L'inductance est une mesure de la résistance du circuit à un changement de courant. Un inducteur avec une inductance élevée peut donc être utilisés pour s'opposer à un courant alternatif[1].
Autres composants de circuit
| Composant | Fonction principale | Symbole schématique |
|---|---|---|
| Résistance | S'oppose au passage du courant | |
| Batterie | Agit comme une source d'alimentation | |
| Source de tension continue | Agit comme une source de courant continu (un courant constant qui circule toujours dans le même sens) |  |
| Source de tension alternative | Agit comme une source de courant alternatif (un courant variable dont le sens de circulation s'inverse périodiquement) |  Crédit image: licence CC BY-SA 4.0 🛈 |
| Diode | Permet au courant de circuler facilement dans un sens mais pas dans l'autre | 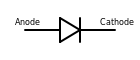 Crédit image: licence CC BY-SA 3.0 🛈 |
| Condensateur | Emmagasine de l'énergie dans des champs électriques ; emmagasine des charges électriques ; permet le passage d'un courant alternatif de fréquence faible |  |
| Bobine d'inductance | Emmagasine de l'énergie dans les champs magnétiques ; s'oppose aux changements de courant |
Lois des circuits
Loi des nœuds (en haut) : I1 + I2 + I3 = I4 + I5
Loi des mailles (en bas) : U1 + U2 + U3 + U4 = 0La théorie des circuits traite des circuits (ou réseaux) électriques, pour lesquels les champs sont largement confinés autour des conducteurs de courant. Dans de tels circuits, des lois simples peuvent être utilisées au lieu de dériver le comportement du circuit directement à partir des lois de l'électromagnétisme. La loi d'Ohm énonce la relation entre le courant et la tension d'un circuit en introduisant deux quantités appelées résistance et conductance [30] : La puissance électrique est définie comme . La loi d'Ohm peut être utilisée pour fournir la puissance du circuit en termes des autres quantités[31] : La loi de Kirchhoff des nœuds stipule que le courant total qui arrive à une jonction (un nœud) du circuit doit être égal au courant total qui repart de la jonction. Cette loi est une conséquence de la conservation de la charge, car le courant est défini comme un flux de charge dans le temps. Si un courant se sépare en sortie d'un nœud, la somme des courants résultants est égale au courant qui arrive au nœud[32].
La loi de Kirchhoff des mailles stipule que la somme de la tension le long d'une boucle fermée (une maille) d'un circuit est égale à zéro. Cette loi vient du fait que le champ électrique est conservateur, ce qui signifie que quel que soit le chemin emprunté, le potentiel en un point ne change pas lorsqu'on y revient[32].
Ces lois permettent également de retrouver comment additionner des quantités, telles que le courant et la tension, dans les circuits montés en série et montés en parallèle[32].
Dans un montage en série, le courant qui traverse chaque composant est le même, les tensions s'additionnent, de même que les résistances, et les conductances sont liées comme indiqué : Dans un montage en parallèle, la tension aux bornes de chaque composant est la même, les courants s'additionnent, les résistances sont liées comme indiqué, et les conductances s'additionnent :
Notes et références
Notes
- La divergence d’un champ de vecteur en un point de l’espace est un nombre scalaire qui mesure le flux de ce champ de vecteur convergeant en ce point. Par exemple, si le champ de vecteur représente le mouvement de matière dans un fluide, la divergence mesure la quantité de fluide qui s’accumule en ce point, contribuant à y augmenter la densité de fluide si le nombre est positif et à la diminuer s'il est négatif.
- Le rotationnel d’un champ de vecteur en un point de l’espace est un vecteur qui mesure le tourbillonnement du champ de vecteur en ce point. Par exemple si le champ de vecteur représente le mouvement de l’eau dans une rivière, le rotationnel mesure la rotation sur lui-même d'un objet placé en ce point. Si la rivière s’écoule de façon uniforme, l’objet ne tourbillonne pas. Si la rivière s’écoule plus rapidement sur la droite de son lit que sur la gauche, l’objet va se mettre à tourbillonner entre les couches d’eau, à cause des frottements. La direction du vecteur rotationnel indique l’axe de rotation de l’objet (vertical dans notre cas) et sa longueur indique la vitesse de rotation. Le rotationnel est parfois appelé vecteur tourbillon.
Références
- Purcell, Edward M., Electricity and magnetism, Cambridge, Third, , 3–4 p. (ISBN 978-1-107-01402-2, OCLC 805015622, lire en ligne)
- Jimmy Roussel, « Cours de physique : Électromagnétisme » [PDF], , p. 124
- Walker, Jearl, 1945-, Fundamentals of physics, Hoboken, NJ, 9th, , 578 p. (ISBN 978-0-470-46911-8, OCLC 435710913, lire en ligne)
- Pumplin, « Electric field lines », Michigan State University Physics, (consulté le )
- « The Feynman Lectures on Physics Vol. II Ch. 1: Electromagnetism », feynmanlectures.caltech.edu (consulté le )
- « Magnetic forces », hyperphysics.phy-astr.gsu.edu (consulté le )
- Grant, I. S. (Ian S.), Electromagnetism, Chichester [England], 2nd, coll. « The Manchester Physics Series », , 17–22 p. (ISBN 0-471-92711-2, OCLC 21447877, lire en ligne)
- « Gauss's Law », hyperphysics.phy-astr.gsu.edu (consulté le )
- « The Feynman Lectures on Physics Vol. II Ch. 4: Electrostatics, S5: The flux of E », feynmanlectures.caltech.edu (consulté le )
- « Ampere's Law », hyperphysics.phy-astr.gsu.edu (consulté le )
- Grant, I. S. (Ian S.), Electromagnetism, Chichester [England], 2nd, coll. « The Manchester Physics Series », , 125 p. (ISBN 0-471-92711-2, OCLC 21447877, lire en ligne)
- « Magnets and Electromagnets », hyperphysics.phy-astr.gsu.edu (consulté le )
- « Ferromagnetism », hyperphysics.phy-astr.gsu.edu (consulté le )
- (en) Editors, « Unification theories and a theory of everything », Access Science, (DOI 10.1036/1097-8542.BR0814141, lire en ligne)
- Grant, I. S. (Ian S.), Electromagnetism, Chichester [England], 2nd, coll. « The Manchester Physics Series », , 365 p. (ISBN 0-471-92711-2, OCLC 21447877, lire en ligne)
- Maxwell, « A dynamical theory of the electromagnetic field », Philosophical Transactions of the Royal Society of London, vol. 155, , p. 459–512 (DOI 10.1098/rstl.1865.0008, Bibcode 1865RSPT..155..459C, S2CID 186207827, lire en ligne [archive du ]) :
« Light and magnetism are affections of the same substance (p.499) »
- (en-US) « Introduction to the Electromagnetic Spectrum and Spectroscopy | Analytical Chemistry | PharmaXChange.info », pharmaxchange.info, (consulté le )
- « The Feynman Lectures on Physics Vol. II Ch. 13: Magnetostatics », feynmanlectures.caltech.edu (consulté le )
- A. French (1968) Special Relativity, chapter 8 – Relativity and electricity, pp. 229–65, W.W. Norton.
- Hook, J. R., Hall, H. E., Solid State Physics, Chichester, West Sussex, U.K., 2nd, , 76–77 p. (ISBN 978-1-118-72347-0, OCLC 868939953, lire en ligne)
- (en) « What Metals Make Good Conductors of Electricity? », Sciencing (consulté le )
- « The Feynman Lectures on Physics Vol. III Ch. 14: Semiconductors », feynmanlectures.caltech.edu (consulté le )
- (en) « How a Solar Cell Works », American Chemical Society (consulté le )
- « The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity », feynmanlectures.caltech.edu (consulté le )
- « Conductors and Insulators », hyperphysics.phy-astr.gsu.edu (consulté le )
- (en) « Dielectric | physics », Encyclopedia Britannica (consulté le )
- « Dielectrics », hyperphysics.phy-astr.gsu.edu (consulté le )
- Grant, I. S. (Ian S.), Electromagnetism, Chichester [England], 2nd, coll. « The Manchester Physics Series », , 41–42 p. (ISBN 0-471-92711-2, OCLC 21447877, lire en ligne)
- « Ohm's Law », hyperphysics.phy-astr.gsu.edu (consulté le )
- « Electric Power », hyperphysics.phy-astr.gsu.edu (consulté le )
- Young, H. D., Freedman, R. A., Sears and Zemansky's University Physics with Modern Physics, Boston, 14th, , 872–878 p. (ISBN 978-0-321-97361-0, OCLC 897436903, lire en ligne)