Fonction de test pour l'optimisation

En mathématiques appliquées, les fonctions de test sont des fonctions d'évaluation des caractéristiques des algorithmes d'optimisation, telles que taux de convergence ; précision ; robustesse ; performances générales.

Cette page représente que les fonctions de test les plus classiques:

à objectif unique.
multi-objectifs (MOP), avec leurs fronts de Pareto.

Les représentations graphiques sont tirées de Bäck^[1], Haupt et al.^[2] et du logiciel Rody Oldenhuis^[3]. Compte tenu du nombre de problèmes (55 au total), seuls quelques-uns sont présentés ici.

Les fonctions de test utilisées pour évaluer les algorithmes de MOP sont tirées de Deb^[4], Binh et al.^[5] et Binh^[6]. On peut télécharger le logiciel développé par Deb^[7], qui implémente la procédure NSGA-II avec GAs, ou le programme mis en ligne sur Internet^[8], qui implémente la procédure NSGA-II avec ES.

Dans les présentations suivantes, seront juste donnés la forme générale de l'équation, un tracé de la fonction objectif, les limites des variables d'objet et les coordonnées des minima globaux.

Optimisations à objectif unique

Nom	Représentation	Formule	Minimum absolu	Domaine d'application
Rastrigin function	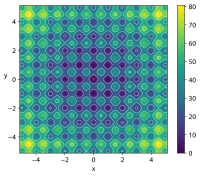Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]$ ${\text{où: }}A=10$	$f(0,\dots ,0)=0$	$-5.12\leq x_{i}\leq 5.12$
Fonction d'Ackley	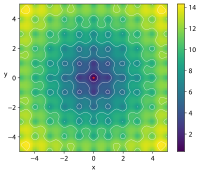Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]$ $-\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Sphère	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}$	$f(x_{1},\dots ,x_{n})=f(0,\dots ,0)=0$	$-\infty \leq x_{i}\leq \infty$ , $1\leq i\leq n$
Rosenbrock function	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]$	${\text{Min}}={\begin{cases}n=2&\rightarrow \quad f(1,1)=0,\\n=3&\rightarrow \quad f(1,1,1)=0,\\n>3&\rightarrow \quad f(\underbrace {1,\dots ,1} _{n{\text{ fois}}})=0\\\end{cases}}$	$-\infty \leq x_{i}\leq \infty$ , $1\leq i\leq n$
Fonction de Beale	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\left(1.5-x+xy\right)^{2}+\left(2.25-x+xy^{2}\right)^{2}$ $+\left(2.625-x+xy^{3}\right)^{2}$	$f(3,0.5)=0$	$-4.5\leq x,y\leq 4.5$
Goldstein–Price	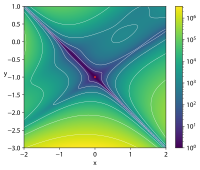Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]$ $\left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]$	$f(0,-1)=3$	$-2\leq x,y\leq 2$
Booth	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\left(x+2y-7\right)^{2}+\left(2x+y-5\right)^{2}$	$f(1,3)=0$	$-10\leq x,y\leq 10$
Bukin N.6	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=100{\sqrt {\left\|y-0.01x^{2}\right\|}}+0.01\left\|x+10\right\|.\quad$	$f(-10,1)=0$	$-15\leq x\leq -5$ , $-3\leq y\leq 3$
Fonction de Matyas	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=0.26\left(x^{2}+y^{2}\right)-0.48xy$	$f(0,0)=0$	$-10\leq x,y\leq 10$
Fonction de Lévi N.13	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\sin ^{2}3\pi x+\left(x-1\right)^{2}\left(1+\sin ^{2}3\pi y\right)$ $+\left(y-1\right)^{2}\left(1+\sin ^{2}2\pi y\right)$	$f(1,1)=0$	$-10\leq x,y\leq 10$
Himmelblau's function	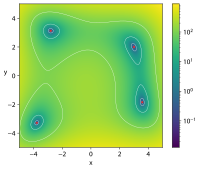Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}.\quad$	${\text{Min}}={\begin{cases}f\left(3.0,2.0\right)&=0.0\\f\left(-2.805118,3.131312\right)&=0.0\\f\left(-3.779310,-3.283186\right)&=0.0\\f\left(3.584428,-1.848126\right)&=0.0\\\end{cases}}$	$-5\leq x,y\leq 5$
Three-hump camel	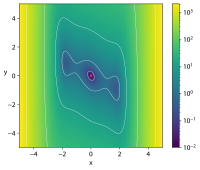Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=2x^{2}-1.05x^{4}+{\frac {x^{6}}{6}}+xy+y^{2}$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Easom	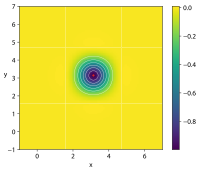Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-\cos \left(x\right)\cos \left(y\right)\exp \left(-\left(\left(x-\pi \right)^{2}+\left(y-\pi \right)^{2}\right)\right)$	$f(\pi ,\pi )=-1$	$-100\leq x,y\leq 100$
Cross-in-tray	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-0.0001\left[\left\|\sin x\sin y\exp \left(\left\|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right\|\right)\right\|+1\right]^{0.1}$	${\text{Min}}={\begin{cases}f\left(1.34941,-1.34941\right)&=-2.06261\\f\left(1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,-1.34941\right)&=-2.06261\\\end{cases}}$	$-10\leq x,y\leq 10$
Eggholder^[9]	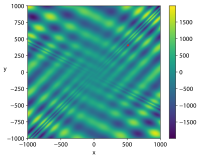Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-\left(y+47\right)\sin {\sqrt {\left\|{\frac {x}{2}}+\left(y+47\right)\right\|}}-x\sin {\sqrt {\left\|x-\left(y+47\right)\right\|}}$	$f(512,404.2319)=-959.6407$	$-512\leq x,y\leq 512$
Table de Hölder	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-\left\|\sin x\cos y\exp \left(\left\|1-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right\|\right)\right\|$	${\text{Min}}={\begin{cases}f\left(8.05502,9.66459\right)&=-19.2085\\f\left(-8.05502,9.66459\right)&=-19.2085\\f\left(8.05502,-9.66459\right)&=-19.2085\\f\left(-8.05502,-9.66459\right)&=-19.2085\end{cases}}$	$-10\leq x,y\leq 10$
McCormick	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\sin \left(x+y\right)+\left(x-y\right)^{2}-1.5x+2.5y+1$	$f(-0.54719,-1.54719)=-1.9133$	$-1.5\leq x\leq 4$ , $-3\leq y\leq 4$
Schaffer N. 2	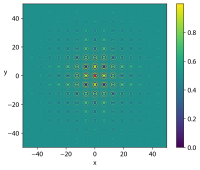Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}$	$f(0,0)=0$	$-100\leq x,y\leq 100$
Schaffer N. 4	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left\|x^{2}-y^{2}\right\|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}$	${\text{Min}}={\begin{cases}f\left(0,1.25313\right)&=0.292579\\f\left(0,-1.25313\right)&=0.292579\\f\left(1.25313,0\right)&=0.292579\\f\left(-1.25313,0\right)&=0.292579\end{cases}}$	$-100\leq x,y\leq 100$
Styblinski–Tang	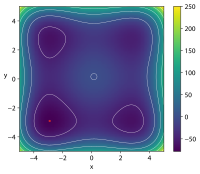Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f({\boldsymbol {x}})={\frac {\sum _{i=1}^{n}x_{i}^{4}-16x_{i}^{2}+5x_{i}}{2}}$	$-39.16617n<f(\underbrace {-2.903534,\ldots ,-2.903534} _{n{\text{ fois}}})<-39.16616n$	$-5\leq x_{i}\leq 5$ , $1\leq i\leq n$ ..

Optimisations contraintes

Name	Plot	Formula	Global minimum	Search domain
Rosenbrock function constrained with a cubic and a line^[10]	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}$ , subjected to: $(x-1)^{3}-y+1\leq 0{\text{ and }}x+y-2\leq 0$	$f(1.0,1.0)=0$	$-1.5\leq x\leq 1.5$ , $-0.5\leq y\leq 2.5$
Rosenbrock function constrained to a disk^[11]	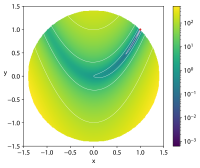Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}$ , subjected to: $x^{2}+y^{2}\leq 2$	$f(1.0,1.0)=0$	$-1.5\leq x\leq 1.5$ , $-1.5\leq y\leq 1.5$
Mishra's Bird function - constrained^[12]^,^[13]	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}$ , subjected to: $(x+5)^{2}+(y+5)^{2}<25$	$f(-3.1302468,-1.5821422)=-106.7645367$	$-10\leq x\leq 0$ , $-6.5\leq y\leq 0$
Townsend function (modified)^[14]	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)$ , subjected to: $x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}$ where: $t = Atan2(x,y)$	$f(2.0052938,1.1944509)=-2.0239884$	$-2.25\leq x\leq 2.25$ , $-2.5\leq y\leq 1.75$
Gomez and Levy function (modified)^[15]	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=4x^{2}-2.1x^{4}+{\frac {1}{3}}x^{6}+xy-4y^{2}+4y^{4}$ , subjected to: $-\sin(4\pi x)+2\sin ^{2}(2\pi y)\leq 1.5$	$f(0.08984201,-0.7126564)=-1.031628453$	$-1\leq x\leq 0.75$ , $-1\leq y\leq 1$
Simionescu function^[16]	Crédit image: Nschloe licence CC BY-SA 4.0 🛈	$f(x,y)=0.1xy$ , subjected to: $x^{2}+y^{2}\leq \left[r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right]^{2}$ ${\text{where: }}r_{T}=1,r_{S}=0.2{\text{ and }}n=8$	$f(\pm 0.84852813,\mp 0.84852813)=-0.072$	$-1.25\leq x,y\leq 1.25$

Optimisations multi-objectifs

Name	Plot	Functions	Constraints	Search domain
Binh and Korn function:	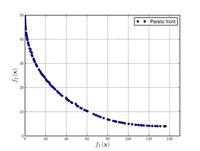Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=4x^{2}+4y^{2}\\f_{2}\left(x,y\right)=\left(x-5\right)^{2}+\left(y-5\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=\left(x-5\right)^{2}+y^{2}\leq 25\\g_{2}\left(x,y\right)=\left(x-8\right)^{2}+\left(y+3\right)^{2}\geq 7.7\\\end{cases}}$	$0\leq x\leq 5$ , $0\leq y\leq 3$
Chankong and Haimes function^[17] :	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=2+\left(x-2\right)^{2}+\left(y-1\right)^{2}\\f_{2}\left(x,y\right)=9x-\left(y-1\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=x^{2}+y^{2}\leq 225\\g_{2}\left(x,y\right)=x-3y+10\leq 0\\\end{cases}}$	$-20\leq x,y\leq 20$
Fonseca–Fleming function^[18] :	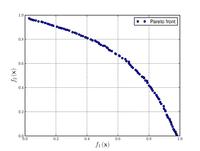Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}$		$-4\leq x_{i}\leq 4$ , $1\leq i\leq n$
Test function 4:	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x^{2}-y\\f_{2}\left(x,y\right)=-0.5x-y-1\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=6.5-{\frac {x}{6}}-y\geq 0\\g_{2}\left(x,y\right)=7.5-0.5x-y\geq 0\\g_{3}\left(x,y\right)=30-5x-y\geq 0\\\end{cases}}$	$-7\leq x,y\leq 4$
Kursawe function:	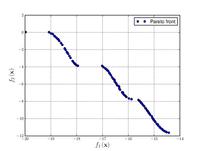Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left\|x_{i}\right\|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}$		$-5\leq x_{i}\leq 5$ , $1\leq i\leq 3$ .
Schaffer function N. 1^[19] :	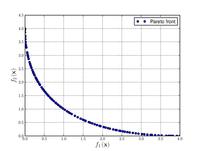Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)=x^{2}\\f_{2}\left(x\right)=\left(x-2\right)^{2}\\\end{cases}}$		$-A\leq x\leq A$ . Values of $A$ from $10$ to $10^{5}$ have been used successfully. Higher values of $A$ increase the difficulty of the problem.
Schaffer function N. 2:	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)={\begin{cases}-x,&{\text{if }}x\leq 1\\x-2,&{\text{if }}1<x\leq 3\\4-x,&{\text{if }}3<x\leq 4\\x-4,&{\text{if }}x>4\\\end{cases}}\\f_{2}\left(x\right)=\left(x-5\right)^{2}\\\end{cases}}$		$-5\leq x\leq 10$ .
Poloni's two objective function:	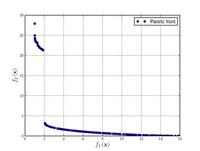Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}$ ${\text{where}}={\begin{cases}A_{1}=0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\A_{2}=1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\B_{1}\left(x,y\right)=0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\B_{2}\left(x,y\right)=1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{cases}}$		$-\pi \leq x,y\leq \pi$
Zitzler–Deb–Thiele's function N. 1^[20] :	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Zitzler–Deb–Thiele's function N. 2^[20] :	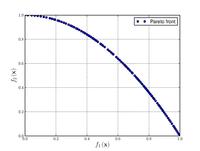Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Zitzler–Deb–Thiele's function N. 3^[20]:	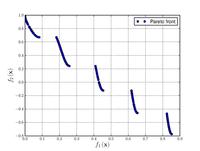Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)\sin \left(10\pi f_{1}\left({\boldsymbol {x}}\right)\right)\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Zitzler–Deb–Thiele's function N. 4^[20]:	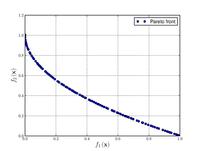Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=91+\sum _{i=2}^{10}\left(x_{i}^{2}-10\cos \left(4\pi x_{i}\right)\right)\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\end{cases}}$		$0\leq x_{1}\leq 1$ , $-5\leq x_{i}\leq 5$ , $2\leq i\leq 10$
Zitzler–Deb–Thiele's function N. 6^[20]:	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 10$ .
Osyczka and Kundu function^[21]:	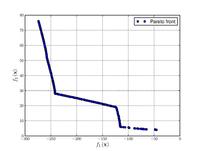Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=-25\left(x_{1}-2\right)^{2}-\left(x_{2}-2\right)^{2}-\left(x_{3}-1\right)^{2}-\left(x_{4}-4\right)^{2}-\left(x_{5}-1\right)^{2}\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{6}x_{i}^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left({\boldsymbol {x}}\right)=x_{1}+x_{2}-2\geq 0\\g_{2}\left({\boldsymbol {x}}\right)=6-x_{1}-x_{2}\geq 0\\g_{3}\left({\boldsymbol {x}}\right)=2-x_{2}+x_{1}\geq 0\\g_{4}\left({\boldsymbol {x}}\right)=2-x_{1}+3x_{2}\geq 0\\g_{5}\left({\boldsymbol {x}}\right)=4-\left(x_{3}-3\right)^{2}-x_{4}\geq 0\\g_{6}\left({\boldsymbol {x}}\right)=\left(x_{5}-3\right)^{2}+x_{6}-4\geq 0\end{cases}}$	$0\leq x_{1},x_{2},x_{6}\leq 10$ , $1\leq x_{3},x_{5}\leq 5$ , $0\leq x_{4}\leq 6$ .
CTP1 function (2 variables)^[4]^,^[22]:	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)=\left(1+y\right)\exp \left(-{\frac {x}{1+y}}\right)\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.858\exp \left(-0.541f_{1}\left(x,y\right)\right)}}\geq 1\\g_{2}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.728\exp \left(-0.295f_{1}\left(x,y\right)\right)}}\geq 1\end{cases}}$	$0\leq x,y\leq 1$ .
Constr-Ex problem^[4]:	Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)={\frac {1+y}{x}}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=y+9x\geq 6\\g_{2}\left(x,y\right)=-y+9x\geq 1\\\end{cases}}$	$0.1\leq x\leq 1$ , $0\leq y\leq 5$
Viennet function:	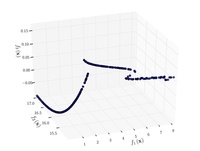Crédit image: Gaortizg licence CC BY-SA 3.0 🛈	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=0.5\left(x^{2}+y^{2}\right)+\sin \left(x^{2}+y^{2}\right)\\f_{2}\left(x,y\right)={\frac {\left(3x-2y+4\right)^{2}}{8}}+{\frac {\left(x-y+1\right)^{2}}{27}}+15\\f_{3}\left(x,y\right)={\frac {1}{x^{2}+y^{2}+1}}-1.1\exp \left(-\left(x^{2}+y^{2}\right)\right)\\\end{cases}}$		$-3\leq x,y\leq 3$ .

Voir aussi

Fonction d'Ackley
Fonction de Himmelblau
Fonction Rastrigin
Fonction de Rosenbrock
Fonction shekel
Fonction binh

Références

↑ Thomas Bäck, Evolutionary algorithms in theory and practice : evolution strategies, evolutionary programming, genetic algorithms, Oxford, Oxford University Press, 1995 (ISBN 978-0-19-509971-3), p. 328
↑ Randy L. Haupt, Sue Ellen Haupt, Practical genetic algorithms with CD-Rom, New York, 2nd, 2004 (ISBN 978-0-471-45565-3)
↑ Oldenhuis, « Many test functions for global optimizers », Mathworks (consulté le 1^er novembre 2012)
↑ ^{a b c d et e} Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. (ISBN 0-471-87339-X).
↑ Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176–182
↑ ^{a et b} Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany
↑ Deb K. (2011) Software for multi-objective NSGA-II code in C. Available at URL: https://www.iitk.ac.in/kangal/codes.shtml
↑ Ortiz, « Multi-objective optimization using ES as Evolutionary Algorithm. », Mathworks (consulté le 1^er novembre 2012)
↑ Whitley, Rana, Dzubera et Mathias, « Evaluating evolutionary algorithms », Artificial Intelligence, Elsevier BV, vol. 85, n^os 1-2,‎ 1996, p. 264 (ISSN 0004-3702, DOI 10.1016/0004-3702(95)00124-7)
↑ Simionescu, P.A. et Beale, D. « New Concepts in Graphic Visualization of Objective Functions » (September 29 – October 2, 2002) (lire en ligne, consulté le 7 janvier 2017)
—ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference
↑ « Solve a Constrained Nonlinear Problem - MATLAB & Simulink », www.mathworks.com (consulté le 29 août 2017)
↑ « Bird Problem (Constrained) | Phoenix Integration » [archive du 29 décembre 2016] (consulté le 29 août 2017)
↑ Mishra, « Some new test functions for global optimization and performance of repulsive particle swarm method », MPRA Paper,‎ 2006 (lire en ligne)
↑ Townsend, « Constrained optimization in Chebfun », chebfun.org, janvier 2014 (consulté le 29 août 2017)
↑ Simionescu, « A collection of bivariate nonlinear optimisation test problems with graphical representations », International Journal of Mathematical Modelling and Numerical Optimisation, vol. 10, n^o 4,‎ 2020, p. 365–398 (DOI 10.1504/IJMMNO.2020.110704)
↑ P.A. Simionescu, Computer Aided Graphing and Simulation Tools for AutoCAD Users, Boca Raton, FL, 1st, 2014 (ISBN 978-1-4822-5290-3)
↑ Vira Chankong et Yacov Y. Haimes, Multiobjective decision making. Theory and methodology., 1983 (ISBN 0-444-00710-5)
↑ Fonseca et Fleming, « An Overview of Evolutionary Algorithms in Multiobjective Optimization », Evol Comput, vol. 3, n^o 1,‎ 1995, p. 1–16 (DOI 10.1162/evco.1995.3.1.1, S2CID 8530790, CiteSeer^x 10.1.1.50.7779)
↑ J. David Schaffer, Proceedings of the First International Conference on Genetic Algorithms, 1984 (OCLC 20004572), « Multiple Objective Optimization with Vector Evaluated Genetic Algorithms »
↑ ^{a b c d et e} Kalyan Deb, L. Thiele, Marco Laumanns et Eckart Zitzler, Proceedings of the 2002 IEEE Congress on Evolutionary Computation, vol. 1, 2002, 825–830 p. (ISBN 0-7803-7282-4, DOI 10.1109/CEC.2002.1007032, S2CID 61001583), « Scalable multi-objective optimization test problems »
↑ Osyczka et Kundu, « A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm », Structural Optimization, vol. 10, n^o 2,‎ 1^er octobre 1995, p. 94–99 (ISSN 1615-1488, DOI 10.1007/BF01743536, S2CID 123433499)
↑ Jimenez, Gomez-Skarmeta, Sanchez et Deb, « An evolutionary algorithm for constrained multi-objective optimization », Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600), vol. 2,‎ mai 2002, p. 1133–1138 (ISBN 0-7803-7282-4, DOI 10.1109/CEC.2002.1004402, S2CID 56563996)

Portail des mathématiques

Dernière mise à jour du contenu le 20/01/2025.

Droit d'auteur : le texte de l'article est disponible sous la licence CC BY-SA 3.0.
Les détails concernant les licences et crédits des images sont disponibles en cliquant sur l'image.

Le site Wikimonde est un agrégateur d'articles encyclopédiques, il n'est pas à l'origine du contenu des articles, ni des images.

Le contenu de cet article est une copie de l'article d'origine (//fr.wikipedia.org/wiki/Fonction_de_test_pour_l%27optimisation) publié sur Wikipédia (wiki collaboratif publié sous licence libre).
Le contenu des articles n'est pas garanti.
Le texte des articles n'est pas modifié par Wikimonde. Des modifications mineures de mise en page et des liens internes (pour faciliter la navigation) peuvent être effectués automatiquement.

Des crédits concernant les images peuvent être ajoutés automatiquement selon les informations fournis par le site d'origine.
Les images sont chargées depuis des sites externes, certaines peuvent ne pas s'afficher.

Auteurs de cet article « Fonction de test pour l'optimisation » :

WikiCleanerBot, Dhatier, TigH, Cbigorgne, Goel, Jilucorg, Mctir9.

[1] Thomas Bäck, Evolutionary algorithms in theory and practice : evolution strategies, evolutionary programming, genetic algorithms, Oxford, Oxford University Press, 1995 (ISBN 978-0-19-509971-3), p. 328

[2] Randy L. Haupt, Sue Ellen Haupt, Practical genetic algorithms with CD-Rom, New York, 2nd, 2004 (ISBN 978-0-471-45565-3)

[3] Oldenhuis, « Many test functions for global optimizers », Mathworks (consulté le 1^er novembre 2012)

[Deb:2002-4] {a b c d et e} Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. (ISBN 0-471-87339-X).

[Binh97-5] Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176–182

[Binh99-6] {a et b} Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany

[Deb_nsga-7] Deb K. (2011) Software for multi-objective NSGA-II code in C. Available at URL: https://www.iitk.ac.in/kangal/codes.shtml

[8] Ortiz, « Multi-objective optimization using ES as Evolutionary Algorithm. », Mathworks (consulté le 1^er novembre 2012)

[Whitley_Rana_Dzubera_Mathias_1996_pp._245–276-9] Whitley, Rana, Dzubera et Mathias, « Evaluating evolutionary algorithms », Artificial Intelligence, Elsevier BV, vol. 85, n^os 1-2,‎ 1996, p. 264 (ISSN 0004-3702, DOI 10.1016/0004-3702(95)00124-7)

[10] Simionescu, P.A. et Beale, D. « New Concepts in Graphic Visualization of Objective Functions » (September 29 – October 2, 2002) (lire en ligne, consulté le 7 janvier 2017)
—ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference

[11] « Solve a Constrained Nonlinear Problem - MATLAB & Simulink », www.mathworks.com (consulté le 29 août 2017)

[12] « Bird Problem (Constrained) | Phoenix Integration » [archive du 29 décembre 2016] (consulté le 29 août 2017)

[13] Mishra, « Some new test functions for global optimization and performance of repulsive particle swarm method », MPRA Paper,‎ 2006 (lire en ligne)

[14] Townsend, « Constrained optimization in Chebfun », chebfun.org, janvier 2014 (consulté le 29 août 2017)

[15] Simionescu, « A collection of bivariate nonlinear optimisation test problems with graphical representations », International Journal of Mathematical Modelling and Numerical Optimisation, vol. 10, n^o 4,‎ 2020, p. 365–398 (DOI 10.1504/IJMMNO.2020.110704)

[16] P.A. Simionescu, Computer Aided Graphing and Simulation Tools for AutoCAD Users, Boca Raton, FL, 1st, 2014 (ISBN 978-1-4822-5290-3)

[17] Vira Chankong et Yacov Y. Haimes, Multiobjective decision making. Theory and methodology., 1983 (ISBN 0-444-00710-5)

[FonzecaFleming:1995-18] Fonseca et Fleming, « An Overview of Evolutionary Algorithms in Multiobjective Optimization », Evol Comput, vol. 3, n^o 1,‎ 1995, p. 1–16 (DOI 10.1162/evco.1995.3.1.1, S2CID 8530790, CiteSeer^x 10.1.1.50.7779)

[Schaffer:1984-19] J. David Schaffer, Proceedings of the First International Conference on Genetic Algorithms, 1984 (OCLC 20004572), « Multiple Objective Optimization with Vector Evaluated Genetic Algorithms »

[Debetal2002testpr-20] {a b c d et e} Kalyan Deb, L. Thiele, Marco Laumanns et Eckart Zitzler, Proceedings of the 2002 IEEE Congress on Evolutionary Computation, vol. 1, 2002, 825–830 p. (ISBN 0-7803-7282-4, DOI 10.1109/CEC.2002.1007032, S2CID 61001583), « Scalable multi-objective optimization test problems »

[OsyczkaKundu1995-21] Osyczka et Kundu, « A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm », Structural Optimization, vol. 10, n^o 2,‎ 1^er octobre 1995, p. 94–99 (ISSN 1615-1488, DOI 10.1007/BF01743536, S2CID 123433499)

[Jimenezetal2002-22] Jimenez, Gomez-Skarmeta, Sanchez et Deb, « An evolutionary algorithm for constrained multi-objective optimization », Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600), vol. 2,‎ mai 2002, p. 1133–1138 (ISBN 0-7803-7282-4, DOI 10.1109/CEC.2002.1004402, S2CID 56563996)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]