Entier naturel

En mathématiques, un entier naturel, un nombre naturel^[1],[2],[3] ou parfois simplement un naturel^[2],[3] est un nombre permettant fondamentalement de compter des objets considérés comme des unités équivalentes : un jeton, deux jetons… une carte, deux cartes, trois cartes… Un tel nombre entier peut s'écrire avec une suite finie de chiffres en toute notation positionnelle de base entière (sans signe et sans virgule), et notamment en notation décimale positionnelle.

L’étude des entiers naturels est l’objet de l’arithmétique, branche des mathématiques dont l'origine remonte à l'Antiquité grecque. Chaque nombre entier a un successeur unique, c'est-à-dire un entier qui lui est immédiatement supérieur, et la liste des entiers naturels est infinie^{[n 1]}.

Les définitions modernes d’entier naturel sont fondées sur :

• l’axiomatisation de l’arithmétique réalisée par Peano et Dedekind à la fin du XIX^e siècle ;
• la construction d’ensembles vérifiant les axiomes de l’arithmétique : Ernst Zermelo, quand il a axiomatisé la théorie des ensembles, a montré que les entiers naturels pouvaient être définis en termes ensemblistes (on utilise aujourd'hui le plus souvent une méthode due à von Neumann).

Les entiers naturels forment un ensemble, communément désigné par le sigle ${\displaystyle \mathbb {N} }$. Ils s'identifient aux entiers relatifs positifs (ou nuls), ainsi qu'aux nombres rationnels positifs (ou nuls) pouvant s'écrire sous la forme d'une fraction de dénominateur 1, et d'une manière plus générale aux réels positifs (ou nuls) de partie fractionnaire nulle.

La définition originelle de l'ensemble des entiers naturels, due à Richard Dedekind^[4], ne comprend pas le nombre zéro^{[n 2]}. Plus récemment, une autre définition a été proposée qui inclut zéro. Ces deux définitions coexistent encore aujourd'hui^[5]. Selon les acceptions, la liste des entiers naturels est donc :

• 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11…

ou

• 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11…

Quelle que soit la définition choisie, (entiers commençant à zéro ou commençant à un), l'ensemble des entiers naturels est conventionnellement noté « ${\displaystyle \mathbf {N} }$ » ou « ${\displaystyle \mathbb {N} }$ », avec tous les risques induits de mésinterprétation. La notation est due à Dedekind en 1888, qui l'utilise pour l'ensemble des entiers commençant à un.

Ainsi, dans les ouvrages qui incluent 0 dans les entiers naturels— c'est le cas dans la majorité des ouvrages scolaires en France —, on trouve les notations ${\displaystyle \mathbb {N} =\{0,1,2,\dots \}}$ et ${\displaystyle \mathbb {N} ^{*}=\{1,2,\dots \}}$

Tandis que, dans les ouvrages qui font commencer les entiers naturels à 1, on trouve la notation ${\displaystyle \mathbb {N} =\{1,2,\dots \}}$ et l'ensemble ${\displaystyle \{0,1,2,\dots \}}$ est alors noté ${\displaystyle \mathbb {W} }$ (whole numbers) ou ${\displaystyle \mathbb {Z} _{+}}$ (entiers relatifs positifs ou nuls) ou ${\displaystyle \mathbb {N} _{0}}$^{[réf. souhaitée]}.

On trouve aussi des notations moins ambiguës exposées dans la section Notations.

La notion d'entier naturel, occupant d'abord (et jusqu'au XVII^e siècle^[6]) toute l'idée^{[n 3]} de nombre, est probablement issue de la notion de collection : le nombre entier est avant tout conçu comme un cardinal. Certains objets ou animaux, tout en étant distincts les uns des autres, peuvent admettre une désignation commune, du fait de leur ressemblance ou d'une autre caractéristique partagée. Leur rassemblement constitue une collection, tel un troupeau de vaches, un collier de perles, un tas de pierres.

Le nombre est en germe dans l'énumération d'une collection, c'est-à-dire le fait de faire défiler tous ses éléments, un à un et sans répétition. Il prend consistance dans le constat que deux énumérations simultanées (d'un troupeau vers un enclos et de cailloux dans un sac, par exemple) se terminent soit toujours en même temps, soit toujours en décalage. Le nombre est enfin représenté lorsque le sac de cailloux ou le bâton à encoches est utilisé pour indiquer une quantité.

Cependant, le concept d'entier ne naît véritablement que lorsqu'il est départi de ce qu'il représente, c'est-à-dire lorsqu'il ne représente plus ni cailloux, ni encoches, ni vaches : il y a là une première abstraction où chaque objet est considéré comme une unité pure et sans qualité. Ce processus mental est connu sous le nom d'abstraction : il est fait abstraction de la qualité de l'objet pour s'intéresser uniquement à la quantité. Une seconde abstraction mène alors à la considération de ces unités comme une collection d'unités^{[n 4]}.

Euclide donne au Livre VII des Éléments la définition suivante : « L'unité est ce relativement à quoi tout objet est appelé Un. » Cette abstraction lui permet de définir ensuite le nombre (entier naturel) comme « collection d'unités^{[n 5]} ».

Représentation des premiers entiers naturels non nuls par des collections de points.

0	1	2	3	4	5	6	7	8	9	10

La désignation des entiers dans le langage n'est pas la même d'une langue à l'autre, même si elle se fonde en général sur quelques méthodes simples.

Les premiers entiers ont un nom spécifique sans lien les uns avec les autres. En français, il s'agit des entiers de un à dix (les noms des entiers de onze à seize sont en fait des déformations de noms composés). Certaines langues n'ont pas de mot spécifique au-delà de deux^[7].

L'accolement de deux noms peut désigner le résultat de l'addition (comme dans dix-sept) ou de la multiplication (comme dans quatre-vingts) des entiers correspondants^[8]. D'autres procédés existent utilisant la soustraction, la division ou la protraction.

Certains « grands » nombres reçoivent également un nom spécifique, en général certaines puissances d'une base particulière. La base dix est la plus répandue aujourd'hui, mais la désignation des entiers en français par exemple conserve la trace d'un usage partiel de la base vingt^[8]. Des conventions internationales contradictoires proposent des désignations standardisées pour les cent premières puissances de mille ou du million.

Au-delà des limites imposées par le vocabulaire, la langue ne peut que proposer des désignations par accolement : « mille milliards de milliards… »

L'écriture des entiers a beaucoup varié dans l'histoire des civilisations. Dans tous les cas, elle utilise un nombre limité de chiffres, symbolisant chacun un entier naturel, et des règles de composition permettant de créer, à partir de ces chiffres, les symboles écrits représentant d'autres entiers.

• 

  
  Les entiers de 1 à 12 représentés en chiffres romains : ils sont tous construits à partir des chiffres 1 (I), 5 (V) et 10 (X).
• 

  
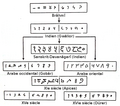
  L'évolution des chiffres indiens puis arabes jusqu'à leur forme contemporaine.
• 
  Chiffres chinois représentant notamment les entiers de 0 à 10.

Le système aujourd'hui le plus répandu est celui de la notation décimale positionnelle : il utilise dix chiffres, dits "arabes" et notés (0,1,2,3,4,5,6,7,8 et 9)^{[n 6]}, et, comme chaque entier naturel se décompose de façon unique en une somme de multiples de puissances de dix de façon que chaque coefficient multiplicateur soit strictement inférieur à dix, l'écriture de tout nombre entier supérieur à 9 se fait en accolant ces chiffres rangés par ordre décroissant des puissances de 10 correspondantes.

Ainsi, par exemple, on écrit : ${\displaystyle 1984=1\times 1000+9\times 100+8\times 10+4=1\times 10^{3}+9\times 10^{2}+8\times 10^{1}+4\times 10^{0}}$.

La pratique du calcul a pu s'appuyer sur la manipulation de cailloux ou d'autres symboles concrets^{[n 7]}, d'abord pour symboliser une unité par caillou, puis en différenciant la valeur des symboles (un coquillage dénotant par exemple dix cailloux).

La notation positionnelle a permis de différencier les valeurs des symboles en fonction de leur position et non plus leur nature, ce qui s'est traduit par le développement de l'abaque et du boulier. Ce principe est toujours en vigueur dans les calculatrices et ordinateurs.

Dès l'Antiquité, les entiers naturels et leurs propriétés sont étudiés par des mathématiciens : les travaux de l'école pythagoricienne^[9] et ceux d'Euclide ont définissent ainsi les bases de l'arithmétique élémentaire^[10], encore enseignée aujourd'hui dans le primaire^[11] et une grande partie du secondaire^[12].

L'arithmétique élémentaire considère que le concept d'entier et ceux d'addition comme de multiplication sont admis^[13]. Plusieurs de leurs propriétés sont également admises, comme celles illustrées par les exemples ci-dessous :

• on peut ranger les entiers par ordre croissant (en langage mathématique moderne : l'ensemble des entiers est bien ordonné)
• ${\displaystyle 2+3=3+2}$ et ${\displaystyle 2\times 3=3\times 2}$ (en langage mathématique moderne : l'addition est commutative, ainsi que la multiplication)
• ${\displaystyle 2+3+4=(2+3)+4=2+(3+4)}$ (en langage mathématique moderne : l'addition est associative)
• ${\displaystyle 2\times (3+4)=2\times 3+2\times 4}$ (en langage mathématique moderne : la multiplication est distributive par rapport à l'addition)

De l'addition est déduite la soustraction, et de la multiplication la division euclidienne.

Crédit image:

AmericanXplorer13 sur Wikipédia anglais

licence CC BY-SA 3.0 🛈

Les raisonnements des mathématiciens antiques, souvent appuyés sur la géométrie^[14], et ceux de leurs successeurs, permettent d'énoncer un très grand nombre de propriétés des nombres entiers, dont certaines sont indiquées ci-dessous :

• infinité d'entiers : il existe un nombre infini d'entiers ;
• nombres premiers : il existe une infinité d'entiers, appelés nombres premiers, qui ne sont divisibles que par 1 et par eux-mêmes^[15] ;
• décomposition en facteurs premiers : tout entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon, à l'ordre près des facteurs^[10]. C'est le théorème fondamental de l'arithmétique, qui permet aussi de définir le pgcd et le ppcm de deux entiers ;
• triplets pythagoriciens : il existe une infinité de triplets d'entiers non nuls (${\displaystyle a,b,c}$) premiers entre eux qui vérifient la relation de Pythagore : ${\displaystyle a^{2}+b^{2}=c^{2}}$.

En représentant chaque entier par une collection d'objets (des cailloux ou des jetons par exemple), l'opération d'addition correspond à réunir deux collections, tandis que la soustraction revient à retirer une collection d'une autre, ce qui montre l'impossibilité de soustraire (dans les entiers naturels^{[n 8]}) un nombre à un autre strictement plus petit.

La multiplication de deux entiers naturels correspond au remplissage d'un rectangle dont deux côtés adjacents représentent chacun l'un des facteurs. Cette correspondance met en évidence la relation qui existe, pour les nombres entiers naturels, entre addition et multiplication^{[n 9]}. Par exemple , multiplier 2 par 3 est équivalent à additionner 2 deux fois avec lui-même : ${\displaystyle 2\times 3=2+2+2}$.

La division euclidienne d'un entier (appelé dividende) par un autre (appelé diviseur et nécessairement non nul) est illustrée par le rangement de la collection représentant le dividende en un rectangle dont un côté représente le diviseur. Le nombre de rangées complètes représente alors le quotient tandis que l'éventuelle rangée incomplète représente le reste, nécessairement strictement inférieur au diviseur.

Étant donné un entier naturel non nul, l’ensemble de ses multiples est infini mais régulièrement réparti et facile à décrire par une suite arithmétique. Par exemple, les multiples de 2 sont les nombres pairs, qui sont alternés avec les nombres impairs parmi tous les entiers.

Au contraire, l’ensemble des diviseurs d’un entier non nul est toujours fini et sa répartition n’a pas du tout le même genre de régularité. Il contient certes toujours le nombre à diviser et le nombre 1, les éventuels autres diviseurs se situant entre ces deux extrêmes. Mais il est en général difficile de lister ces autres diviseurs à partir d’une écriture du nombre dans une base donnée.

Ce problème est lié en partie à la rareté de critères simples pour déterminer sans calcul si un nombre est divisible par un autre. Dans un système de numération positionnelle décimale, plusieurs critères de divisibilité sont connus pour de petits diviseurs (surtout pour 2, 3, 5, 9 et 10), mais en dehors de ces quelques cas, c’est essentiellement la division euclidienne qui permet de répondre à cette question.

Depuis la fin du XIX^e siècle, plusieurs mathématiciens se sont intéressés à la définition formelle des entiers, de leur ensemble, de certaines de leurs propriétés, et à la notation correspondante.

Quelle que soit la manière d’introduire les entiers naturels, l’existence d’un ensemble les contenant tous, repose sur une forme ou une autre de l’axiome de l’infini.

Si les entiers naturels sont introduits avant la théorie des ensembles, celle-ci étant construite comme une extension de l’arithmétique, l’axiome de l’infini sous sa forme la plus simple énonce : il existe au moins un ensemble (infini) contenant tous les entiers naturels^[16]. D’où l’existence de l’ensemble des entiers naturels par application de l’axiome de compréhension.

Si les entiers naturels sont introduits comme les cardinaux finis, l’existence peut être démontrée à partir de l’axiome : il existe au moins un ensemble infini^[17]. On montre que tout cardinal fini est inférieur au cardinal d’un ensemble infini. Par ailleurs le schéma d'axiomes de remplacement permet de montrer que pour tout cardinal, il existe un ensemble des cardinaux qui lui sont inférieurs. L’ensemble des cardinaux inférieurs au cardinal d’un ensemble infini contient donc tous les entiers naturels.

Si les entiers naturels sont introduits par la méthode de Von Neumann, l’existence résulte directement de l’axiome de l’infini sous la forme : Il existe un ensemble auquel appartient l'ensemble vide et qui est clos par application du successeur x ↦ x ∪ {x} . L’ensemble des entiers naturels est alors l’intersection de tous les ensembles vérifiant cette propriété.

N ${\displaystyle ,\mathrm {I_{\,}\!\!N} ,\mathbb {N} ,\mathbb {N} ^{*},\mathbb {N} _{1}}$ pour ${\displaystyle \{1,2,\ldots \}}$

N, ${\displaystyle \mathrm {I_{\,}\!\!N} ,\mathbb {N} ,\mathbb {N} _{0}}$ pour ${\displaystyle \{0,1,2,\ldots \}}$

${\displaystyle \mathbb {N} _{\neq 0},\mathbb {N} _{>0}}$ pour ${\displaystyle \{1,2,\ldots \}}$

${\displaystyle \mathbb {N} _{\geq 0}}$ pour ${\displaystyle \{0,1,2,\ldots \}}$

Différentes notations pour l'ensemble des entiers, comprenant ou non zéro.

En 1894, Giuseppe Peano utilise les notations « N » pour « nombre entier strictement positif » et « N₀ » pour « nombre entier positif ou nul » dans ses Notations de logique mathématique^[18] qui servent d'introduction à son grand projet de formalisation des mathématiques, le Formulaire de mathématiques^[19]. Il l'utilise comme prédicat une notion très proche de celle d'ensemble. Ainsi Peano écrit « x ε N » (qu'on écrit aujourd'hui « ${\displaystyle x\in \mathbb {N} }$ ») ce qui pour lui se lit « x est un nombre entier strictement positif ».

La notation historique de l'ensemble des entiers naturels en imprimerie devient « N », lettre capitale grasse. En écriture manuscrite (et particulièrement au tableau noir), ce caractère a été distingué de la lettre « N » utilisée pour d'autres usages par le doublement de la première barre verticale, ou de la barre oblique, « ${\displaystyle \mathbb {N} }$ ». Ce dernier choix a été adopté pour la police gras de tableau noir. L'édition mathématique moderne utilise maintenant les caractères « doublés », mais l'usage du gras typographique perdure également.

Frege a songé (dans Les Fondements de l'arithmétique, 1884) à définir les entiers en termes de classe de bijectabilité.

Cette idée consiste à définir chaque entier n comme le rassemblement de tous les ensembles ayant n éléments.

Cette très séduisante définition se heurte au paradoxe de Russell si l'on souhaite, en vue d'un monisme ontologique, qu'un tel rassemblement soit, aussi, un ensemble.

Ceci car, sauf pour l'entier 0, identifié à l'ensemble contenant uniquement l'ensemble vide, pour tout autre entier n le rassemblement des ensembles ayant n éléments est une classe propre et donc n'est pas un ensemble.

La définition de Frege conduit donc à une impasse^[20]. Pour en sortir, les mathématiciens ont cherché à définir un représentant dans chaque classe de bijectabilité, appelé cardinal de chacun des éléments de la classe. Cela peut être réalisé par le τ de Hilbert^[17] ou par un axiome adéquat garantissant la possibilité du choix d’un tel représentant dans chaque classe de bijectabilité^[21]. Un cardinal a est dit fini s’il est différent de a + 1. Les entiers naturels sont définis comme les cardinaux finis.

• 0 = Card (∅)
• 1 = Card ({a})
• 2 = Card ({a, b})

Les entiers naturels peuvent être définis comme des ordinaux, c'est-à-dire, par la méthode de von Neumann, comme des ensembles bien ordonnés tous comparables par inclusion. Les entiers naturels sont les ordinaux finis, ceux dont l'ordre réciproque est aussi un bon ordre, ou encore les ordinaux successeurs dont tous les minorants sont aussi des ordinaux successeurs.

Le plus petit ordinal infini est la borne supérieure de tous les ordinaux finis, qui sont les entiers naturels. Il a été introduit par Georg Cantor qui l'a noté ω (lettre minuscule grecque oméga) ou ω₀^[22]. John von Neumann a montré que les ordinaux pouvaient être définis de façon à identifier un ordinal à l'ensemble de ses minorants stricts, et l'ordinal ω s'identifie alors à l'ensemble des entiers naturels (un entier naturel étant lui-même identifié à l'ensemble des entiers naturels qui lui sont strictement inférieurs). En théorie des ensembles, la lettre ω est donc aussi utilisée pour désigner l'ensemble des entiers naturels. L'axiome de l'infini permet de montrer l'existence de cet ensemble.

Un ensemble dénombrable est un ensemble qui a même cardinal que l'ensemble des entiers naturels (on précise parfois « infini dénombrable », dénombrable pouvant aussi signifier « fini ou de même cardinal que ${\displaystyle \mathbb {N} }$ »). Le cardinal du dénombrable, celui de ${\displaystyle \mathbb {N} }$, est le plus petit cardinal infini, il est noté ℵ₀, aleph-zéro.

Quelle que soit la façon d'introduire les entiers naturels, ceux-ci ont les mêmes propriétés fondamentales à partir desquelles on développe l'arithmétique. Richard Dedekind et Giuseppe Peano en ont proposé indépendamment des axiomatisations qui étaient essentiellement équivalentes^[23]. Il s'agissait d'axiomatisation que l'on dit parfois aujourd'hui du second ordre : la notion d'ensemble (ou de prédicat) est supposée connue et n'est pas prise en compte par l'axiomatisation. Voici une présentation moderne de ces axiomes (dits axiomes de Peano)^[24] :

1. L'élément appelé zéro et noté 0, est un entier naturel^{[n 10]} ;
2. Tout entier naturel n a un unique successeur, souvent noté s(n) ou S n (ou autres variantes) ;
3. Aucun entier naturel n'a 0 pour successeur ;
4. Deux entiers naturels ayant même successeur sont égaux ;
5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à ${\displaystyle \mathbb {N} }$.

Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le second que le successeur est une fonction, le quatrième que cette fonction est injective, le troisième qu'il possède un premier élément (ces deux axiomes assurent que l'ensemble des entiers naturels est infini). Le cinquième est une formulation du principe de récurrence.

Une propriété importante, démontrée par Richard Dedekind à partir de ces axiomes, est le principe de définition par récurrence. Il permet par exemple de définir les opérations usuelles.

L'ensemble des entiers naturels peut être doté d'opérations d'addition et de multiplication associatives, commutatives, munies de neutres et satisfaisant une propriété de distributivité : l'ensemble des entiers naturels est donc un semi-anneau. On peut démontrer que l'opération "addition" est entièrement définie par les axiomes de Peano, ainsi que l'opération "multiplication" ^[25]: elles sont donc uniques^{[n 11]}.

Il est ordonné pour la relation d'ordre usuelle induite par l'addition, qui lui donne une structure de bon ordre, c'est-à-dire que toute partie non vide admet un plus petit élément. Cette propriété est à la base du raisonnement par récurrence^[24].

L'ensemble est également muni de la relation de divisibilité qui est un ordre partiel.

Délaissés pendant plusieurs siècles au profit de l'analyse et de la géométrie^[26], l'arithmétique, et notamment les entiers naturels, redeviennent un important sujet d'étude au XIXème siècle, à une époque où de multiples tentatives vont être faites pour trouver des fondements solides aux mathématiques et unifier arithmétique, algèbre et géométrie^{[n 12]}. Leopold Kronecker, l'un des mathématiciens qui relancent l'arithmétique , déclare alors que "Dieu a créé les entiers naturels, tout le reste est création de l'homme" ^[27].

Certains historiens des mathématiques considèrent que les avancées réalisées à cette époque grâce à l'étude des entiers et leur axiomisation sont à la base d'une très grande partie des mathématiques, affirmant même qu'à partir du milieu des années 1800 "les entiers sont devenus le fondement de toutes les mathématiques classiques"^[28] . Le présent chapitre donne, à titre d'exemples des conséquences que les mathématiciens ont tirées de l'étude des entiers, la construction progressive, à partir des entiers, de tous les nombres.

En partant des entiers naturels, les mathématiciens ont pu formellement définir les entiers relatifs et construire leur ensemble, communément appelé ${\displaystyle \mathbb {Z} }$. L'origine de cette construction serait la volonté de définir des nombres tels que, pour tous ${\displaystyle a}$ et ${\displaystyle c}$ donnés, on puisse trouver ${\displaystyle b}$ tel que ${\displaystyle a+b=c}$, ce qui est impossible avec des entiers naturels si ${\displaystyle a>c}$ . Les nombres négatifs ont été utilisés dès l'Antiquité en Asie^{[n 13]}, mais il leur a fallu longtemps pour être admis en Occident^[29] : introduits par la géométrie, leur définition formelle date du XIX^e siècle^[28]. Les nombres relatifs sont alors définis à partir de couples d'entiers naturels et d'une relation d'équivalence. Quant à l'addition comme la multiplication, elles sont déduites de celles définies pour les entiers naturels. L'ensemble ${\displaystyle \mathbb {Z} }$ peut être considéré comme constitué de la réunion de l'ensemble des entiers naturels^{[n 14]}, ${\displaystyle \mathbb {N} }$, et de celui de leurs opposés ${\displaystyle (-\mathbb {N} )}$.

Crédit image:

Petronell Vorster

licence CC BY-SA 4.0 🛈

Les nombres rationnels sont ceux qui peuvent se comprendre comme le quotient de deux entiers, et s'écrire ${\displaystyle a/b}$. Certains d'entre eux étaient connus, souvent comme mesure géométrique, et utilisés dès l'Antiquité, notamment par les Egyptiens. La définition formelle de ces nombres, et la construction de leur ensemble usuellement dénommé ${\displaystyle \mathbb {Q} }$, datent du XIXème siècle, selon une approche partant de ${\displaystyle \mathbb {Z} }$ semblable à celle utilisée pour construire ${\displaystyle \mathbb {Z} }$ à partir de ${\displaystyle \mathbb {N} }$^[28]. Les entiers relatifs appartiennent à ${\displaystyle \mathbb {Q} }$, où ils sont tous les rationnels pouvant s'écrire sous la forme ${\displaystyle a/1}$.

Crédit image:

HB

licence CC BY-SA 4.0 🛈

Les mathématiciens de la Grèce antique savaient déjà que la racine carrée de ${\displaystyle 2}$, qui sera notée ${\displaystyle {\sqrt {2}}}$, ne pouvait être représentée ni calculée par le rapport de deux entiers^[30]. Et, vers 1760, il est démontré que le nombre π ne peut pas l'être non plus. De tels nombres sont dénommés "irrationnels". C'est vers la fin des années 1860 que sont formellement définis les nombres réels, rationnels comme irrationnels, et l'ensemble ${\displaystyle \mathbb {R} }$ qu'ils constituent. Deux méthodes ont été utilisées^[31] : la coupure de Dedekind appliquée à l'ensemble ${\displaystyle \mathbb {Q} }$ des nombres rationnels, et une construction à partir des suites de Cauchy. Et, à partir de couples de nombres réels, les mathématiciens définissent les nombres complexes, dont l'ensemble est communément désigné par ${\displaystyle \mathbb {C} }$.

• Peter J. Bentley, Livre des nombres, leur histoire et leurs secrets, des origines à nos jours, Eyrolles, Paris, 2009, 272 pages, (ISBN 978-2-212-54226-4). Traduction par Anne-Marie Terel et Laurence Nicolaïeff du livre The Book of Numbers, Cassel Illustrated, London, 2008.
• Nicolas Bourbaki, Eléments d'histoire des mathématiques, Paris, Hermann, coll. « Histoire de la pensée », 1960, 284 p. (lire en ligne).
• (en) Florian Cajori, A History of Mathematical Notation, 2 Notations mainly in higher mathematics, Chicago, Open Court Publishing, 1929, 367 p. (lire en ligne).
• Pierre Damphousse, L'arithmétique ou l'art de compter, éditions Le Pommier, 2002.
• Georges Ifrah, Histoire universelle des chiffres, éditions Seghers, Paris, Lausanne, 1981, 567 pages, (ISBN 2-221-50205-1).
• Giuseppe Peano, Formulaire de mathématiques : Logique mathématique, t. 2, Turin, Rivista di Matematica, 1897, 60 p. (lire en ligne).
• Benoît Rittaud, Qu'est ce qu'un nombre ?, Les Petites Pommes du savoir, éditions Le Pommier, Paris, 2011, 64 pages, (ISBN 978-2-7465-0565-0).
• (en) Patrick Suppes, Axiomatic Set Theory, New York, Dover, 1972, 308 p. (ISBN 0-486-61630-4, lire en ligne).

• Carré parfait
• Cube parfait

• Liste de nombres
• Nombre premier
• Nombre chanceux
• Nombre harmonique
• Nombre chromatique
• Nombre triangulaire

Notion de nombre
Ensembles usuels	Entier naturel (${\displaystyle \scriptstyle \mathbb {N} }$) Entier relatif (${\displaystyle \scriptstyle \mathbb {Z} }$) Nombre décimal (${\displaystyle \scriptstyle \mathbb {D} }$) Nombre rationnel (${\displaystyle \scriptstyle \mathbb {Q} }$) Nombre réel (${\displaystyle \scriptstyle \mathbb {R} }$) Nombre complexe (${\displaystyle \scriptstyle \mathbb {C} }$)	Crédit image: David Vignoni (original icon); Flamurai (SVG convertion); bayo (color) licence GPL 🛈
Extensions	Quaternion (${\displaystyle \scriptstyle \mathbb {H} }$) Octonion (${\displaystyle \scriptstyle \mathbb {O} }$) Sédénion (${\displaystyle \scriptstyle \mathbb {S} }$) Nombre complexe déployé Tessarine Nombre bicomplexe (${\displaystyle \scriptstyle \mathbb {C} _{2}}$) Nombre multicomplexe (${\displaystyle \scriptstyle \mathbb {C} _{n}}$ ${\displaystyle \scriptstyle {\mathcal {M}}\mathbb {C} _{n}}$) Biquaternion Coquaternion Quaternion hyperbolique Octonion déployé Nombre hypercomplexe Nombre p-adique (${\displaystyle \scriptstyle \mathbb {Q} _{p}}$) Nombre hyperréel Nombre superréel Entier surnaturel Entier profini Nombre dual Droite réelle achevée Nombre cardinal Nombre ordinal Nombre surréel Nombre pseudo-réel
Propriétés particulières	Parité Nombre premier Nombre composé Nombre figuré Nombre parfait Nombre positif Nombre négatif Fraction dyadique Nombre irrationnel Nombre algébrique Nombre transcendant Nombre imaginaire pur Nombre de Liouville Période Nombre normal Nombre univers Nombre constructible Nombre réel calculable Nombre transfini Infiniment petit
Exemples	Pi (π) Racine carrée de deux (${\displaystyle \scriptstyle {\sqrt {2}}}$) Nombre d’or (φ) Zéro (0) Unité imaginaire (i) Constante de Neper (e) Aleph-zéro (ℵ0) Table de constantes mathématiques
Articles liés	Chiffre Numération Fraction Opération Calcul Algèbre Arithmétique Suite d'entiers Infini (∞) Chiffre significatif

Ensembles d'entiers sur la base de leur divisibilité
Formes de factorisation	Nombre premier Nombre composé Nombre puissant Entier sans facteur carré
Sommes de diviseurs	Nombre parfait Nombre presque parfait Nombre quasi parfait Nombre parfait multiple Nombre hémiparfait Nombre hyperparfait Nombre superparfait Nombre unitairement parfait Nombre semi-parfait Nombre semi-parfait primitif Nombre pratique Nombre abondant Nombre hautement abondant Nombre superabondant Nombre colossalement abondant Nombre déficient Nombre étrange Nombre intouchable
Nombreux diviseurs	Nombre hautement composé Nombre hautement composé supérieur
Autre	Nombres amicaux Nombre sociable Nombre solitaire Nombre sublime Nombre à moyenne harmonique entière Nombre frugal Nombre équidigital Nombre extravagant

Puissances de nombres entiers
Quel que soit a non nul : a0 = 1 Quel que soit n : 1n = 1 4n = 22.n 8n = 23.n 9n = 32.n 16n = 24.n Les valeurs sont accessibles jusqu'à 10 milliards exclu.
Puissances de   2	21 22 23 24 25 26 27 28 29 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233
Puissances de   3	31 32 33 34 35 36 37 38 39 310 311 312 313 314 315 316 317 318 319 320
Puissances de   5	51 52 53 54 55 56 57 58 59 510 511 512 513 514
Puissances de   6	61 62 63 64 65 66 67 68 69 610 611 612
Puissances de   7	71 72 73 74 75 76 77 78 79 710 711
Puissances de 10	101 102 103 104 105 106 107 108 109
Puissances de 11	111 112 113 114 115 116 117 118 119
Puissances de 12	121 122 123 124 125 126 127 128 129
Puissances de 13	131 132 133 134 135 136 137 138
Puissances de 14	141 142 143 144 145 146 147 148
Puissances de 15	151 152 153 154 155 156 157 158
Puissances de 17	171 172 173 174 175 176 177 178
Puissances de 18	181 182 183 184 185 186 187
Puissances de 19	191 192 193 194 195 196 197
Puissances de 20	201 202 203 204 205 206 207
Exponentielle  Histoire des logarithmes et des exponentielles

• Arithmétique et théorie des nombres