Équation de Emden-Chandrasekhar

Crédit image:

Prajaman

licence CC BY-SA 4.0 🛈

En astrophysique l'équation de Emden-Chandrasekhar est une forme non linéaire de l'équation de Poisson décrivant la distribution de masse volumique d'une sphère de gaz isotherme soumise à sa propre force gravitationnelle. Elle est ainsi nommée d'après Robert Emden (1907)^[1] et Subrahmanyan Chandrasekhar^[2],[3].

L'équation s'écrit^[4] :

${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }}$

où ${\displaystyle \xi }$ est le rayon adimensionné et ${\displaystyle \psi }$ est un coefficient lié à la masse volumique de la sphère de gaz par ${\displaystyle \rho =\rho _{c}e^{-\psi }}$, où ${\displaystyle \rho _{c}}$ est la valeur centrale. L'équation n'a pas de solution analytique connue. Si l'on utilise un fluide polytropique au lieu d'un fluide isotherme on obtient l'équation de Lane-Emden. L'hypothèse isotherme est généralement utilisée pour décrire le coeur d'une étoile. L'équation est résolue avec les conditions initiales suivantes :

${\displaystyle \psi =0\quad {\text{et}}\quad {\frac {d\psi }{d\xi }}=0\quad {\text{en}}\quad \xi =0}$

L'équation apparaît également dans d'autres branches de la physique, par exemple dans la théorie de Frank-Kamenetskii en géométrie sphérique. La version relativiste de ce modèle isotherme à symétrie sphérique a été étudiée par Chandrasekhar en 1972^[5].

Pour une étoile gazeuse isotherme, la pression ${\displaystyle p}$ est due à la pression cinétique et à la pression de rayonnement

${\displaystyle p=\rho {\frac {k_{B}}{WH}}T+{\frac {4\sigma }{3c}}T^{4}}$

où

• ${\displaystyle \rho }$ est la masse volumique,
• ${\displaystyle k_{B}}$ est la constante de Boltzmann,
• ${\displaystyle W}$ est la masse molaire moyenne,
• ${\displaystyle H}$ est la masse du proton,
• ${\displaystyle T}$ est la température de l'étoile,
• ${\displaystyle \sigma }$ est la constante de Stefan-Boltzmann,
• ${\displaystyle c}$ est la vitesse de la lumière.

L'équation d'équilibre de l'étoile nécessite un équilibre entre la force de pression et la force gravitationnelle :

${\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left({\frac {r^{2}}{\rho }}{\frac {dp}{dr}}\right)=-4\pi G\rho }$

où ${\displaystyle r}$ est le rayon mesuré à partir du centre et ${\displaystyle G}$ est la constante gravitationnelle. L'équation est réécrite de la façon suivante :

${\displaystyle {\frac {k_{B}T}{WH}}{\frac {1}{r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {d\ln \rho }{dr}}\right)=-4\pi G\rho }$

On utilise les transformations suivantes :

${\displaystyle \psi =\ln {\frac {\rho _{c}}{\rho }},\quad \xi =r\left({\frac {4\pi G\rho _{c}WH}{k_{B}T}}\right)^{1/2}}$

où ${\displaystyle \rho _{c}}$ est la densité centrale de l'étoile.

${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }}$

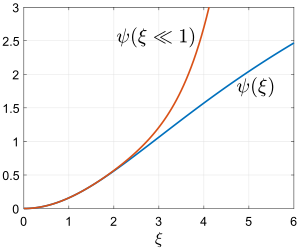
Il n'y a pas de solution analytique connue mais on peut trouver une solution approchée pour ${\displaystyle \xi \ll 1}$ sous forme de développement :

${\displaystyle \psi ={\frac {\xi ^{2}}{6}}-{\frac {\xi ^{4}}{120}}+{\frac {\xi ^{6}}{1890}}+\cdots }$

• On peut se ramener à une équation du premier ordre grâce à une transformation due à Edward Arthur Milne :

${\displaystyle u={\frac {\xi e^{-\psi }}{d\psi /d\xi }},\quad v=\xi {\frac {d\psi }{d\xi }}}$

Ce qui conduit à :

${\displaystyle {\frac {u}{v}}{\frac {dv}{du}}=-{\frac {u-1}{u+v-3}}}$

• Une autre méthode^[6] utilise une fonction singulière donnée par ${\displaystyle x=1/\xi }$. Elle transforme l'équation en :

${\displaystyle x^{4}{\frac {d^{2}\psi }{dx^{2}}}=e^{-\psi }}$

Cette équation possède une solution singulière donnée par :

${\displaystyle e^{-\psi _{s}}=2x^{2}\quad \Rightarrow \quad -\psi _{s}=2\ln x+\ln 2}$

Cela suggère l'introduction d'une nouvelle fonction ${\displaystyle z=-\psi -2\ln x}$ obéissant à :

${\displaystyle {\frac {d^{2}z}{dt^{2}}}-{\frac {dz}{dt}}+e^{z}-2=0\quad {\text{où}}\quad t=\ln x}$

Cette équation peut être réduite au premier ordre en introduisant une nouvelle fonction :

${\displaystyle y={\frac {dz}{dt}}=\xi {\frac {d\psi }{d\xi }}-2}$

On a alors pour cette dernière :

${\displaystyle y{\frac {dy}{dz}}-y+e^{z}-2=0}$

• Si ${\displaystyle \psi (\xi )}$ est une solution de l'équation d'Emden–Chandrasekhar, alors ${\displaystyle \psi (A\xi )-2\ln A}$, où ${\displaystyle A}$ est une constante arbitraire, est aussi une solution de l'équation.
• Les solutions de l'équation qui sont finies à l'origine ont nécessairement ${\displaystyle d\psi /d\xi =0}$ à ${\displaystyle \xi =0}$.

L'hypothèse d'une sphère isotherme représente mal une étoile : la masse volumique obtenue diminue trop lentement à partir du centre pour donner une surface bien définie et une masse finie. On utilise parfois pour ${\displaystyle \xi \gg 1}$ l'approximation suivante^[7] :

${\displaystyle {\frac {\rho }{\rho _{c}}}=e^{-\psi }={\frac {2}{\xi ^{2}}}\left[1+{\frac {A}{\xi ^{1/2}}}\cos \left({\frac {\sqrt {7}}{2}}\ln \xi +\delta \right)+O(\xi ^{-1})\right]}$

où ${\displaystyle A}$ et ${\displaystyle \delta }$ sont des constantes qui sont obtenues à partir d'une solution numérique.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Emden–Chandrasekhar equation » (voir la liste des auteurs).

• Portail de la physique
• Portail de l’astronomie