En mathématiques , la fonction de Gudermann , appelée aussi parfois gudermannien gd , nommée en l'honneur de Christoph Gudermann , fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire intervenir les nombres complexes .
Graphe de la fonction de Gudermann avec ses deux asymptotes horizontales :
θ
=
±
π
2
{\displaystyle \theta =\pm {\frac {\pi }{2}}}
La fonction de Gudermann est définie sur l'ensemble des réels par :
gd
(
t
)
=
∫
0
t
d
u
cosh
u
=
arcsin
(
tanh
t
)
=
signe
(
t
)
⋅
arccos
(
sech
t
)
=
arctan
(
sinh
t
)
=
signe
(
t
)
⋅
arcsec
(
cosh
t
)
=
arccot
(
csch
t
)
=
arccsc
(
coth
t
)
=
2
arctan
(
tanh
t
2
)
=
2
arctan
e
t
−
π
2
.
{\displaystyle {\begin{aligned}{\operatorname {gd} }(t)&=\int _{0}^{t}{\frac {\mathrm {d} u}{\cosh u}}\\&=\arcsin \left(\tanh t\right)=\operatorname {signe} (t)\cdot \arccos \left(\operatorname {sech} t\right)\ \\&=\arctan \left(\sinh t\right)=\operatorname {signe} (t)\cdot \operatorname {arcsec} \left(\cosh t\right)\\&=\operatorname {arccot} \left(\operatorname {csch} t\right)=\operatorname {arccsc} \left(\coth t\right)\\&=2\arctan \left(\tanh {\frac {t}{2}}\right)=2\arctan e^{t}-{\frac {\pi }{2}}.\end{aligned}}}
Le réel
θ
=
gd
(
t
)
{\displaystyle \theta =\operatorname {gd} (t)}
gudermannien de
t
{\displaystyle t}
, est relié à ce dernier par les relations :
sin
θ
=
tanh
t
;
cos
θ
=
1
cosh
t
=
sech
t
;
tan
θ
=
sinh
t
;
tan
θ
2
=
tanh
t
2
.
{\displaystyle {\begin{aligned}{\sin \theta }&=\tanh t~;\quad \cos \theta ={\frac {1}{\cosh t}}=\operatorname {sech} t~;\\\tan \theta &=\sinh t~;\quad \tan {\frac {\theta }{2}}=\tanh {\frac {t}{2}}.\end{aligned}}}
La dérivée de la fonction de Gudermann
t
↦
θ
{\displaystyle t\mapsto \theta }
d
θ
d
t
=
1
cosh
t
=
cos
θ
{\displaystyle {\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {1}{\cosh t}}=\cos \theta }
La fonction de Gudermann est donc la solution s'annulant en 0 de l'équation différentielle
y
′
=
cos
y
{\displaystyle y'=\cos y}
La réciproque de la fonction de Gudermann est définie sur
]
−
π
/
2
,
π
/
2
[
{\displaystyle ]-\pi /2,\pi /2[}
par :
arcgd
(
θ
)
=
g
d
−
1
(
θ
)
=
∫
0
θ
d
u
cos
u
,
=
argtanh
sin
θ
=
signe
(
θ
)
⋅
argcosh
1
cos
θ
,
=
ln
(
tan
θ
+
1
cos
θ
)
=
ln
(
tan
(
θ
2
+
π
4
)
)
,
=
1
2
ln
1
+
sin
θ
1
−
sin
θ
.
{\displaystyle {\begin{aligned}\operatorname {arcgd} (\theta )&={\rm {gd}}^{-1}(\theta )=\int _{0}^{\theta }{\frac {\mathrm {d} u}{\cos u}},\\&=\operatorname {argtanh} \sin \theta =\operatorname {signe} (\theta )\cdot \operatorname {argcosh} {\frac {1}{\cos \theta }},\\&={}\ln \left(\tan \theta +{\frac {1}{\cos \theta }}\right)=\ln \left(\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)\right),\\&={}{\frac {1}{2}}\ln {\frac {1+\sin \theta }{1-\sin \theta }}.\end{aligned}}}
La dérivée de cette fonction réciproque
θ
↦
t
{\displaystyle \theta \mapsto t}
d
t
d
θ
=
1
cos
θ
=
cosh
t
{\displaystyle {\frac {\mathrm {d} t}{\mathrm {d} \theta }}={\frac {1}{\cos \theta }}=\cosh t}
La réciproque de la fonction de Gudermann est donc la solution s'annulant en 0 de l'équation différentielle
y
′
=
cosh
y
{\displaystyle y'=\cosh y}
Applications
Les coordonnées de Mercator d'un point de la sphère sont définies par
x
=
l
o
n
g
i
t
u
d
e
{\displaystyle x=longitude}
y
=
gd
−
1
(
l
a
t
i
t
u
d
e
)
{\displaystyle y=\operatorname {gd} ^{-1}(latitude)}
Elles sont ainsi définies de sorte que les loxodromies de la sphère soient représentées par des droites dans le plan
x
,
y
{\displaystyle x,y}
Le changement de variable
θ
=
gd
(
t
)
{\displaystyle \theta =\operatorname {gd} (t)}
permet de transformer des intégrales de fonctions circulaires en intégrales de fonctions hyperboliques ; par exemple,
∫
0
π
/
2
cos
n
θ
.
d
θ
=
∫
0
+
∞
d
t
cosh
n
+
1
t
{\displaystyle \int _{0}^{\pi /2}{\cos ^{n}\theta .\mathrm {d} \theta }=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{\cosh ^{n+1}t}}}
Ceci explique pourquoi on peut choisir des fonctions circulaires ou hyperboliques lors de changement de variables dans le calcul d'intégrales :
quand on rencontre du
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}}
x
=
cos
θ
{\displaystyle x=\cos \theta }
x
=
1
cosh
t
{\displaystyle x={\frac {1}{\cosh t}}}
x
=
sin
θ
{\displaystyle x=\sin \theta }
x
=
tanh
t
{\displaystyle x=\tanh t}
;
quand on rencontre du
1
+
x
2
{\displaystyle {\sqrt {1+x^{2}}}}
x
=
tan
θ
{\displaystyle x=\tan \theta }
x
=
sinh
t
{\displaystyle x=\sinh t}
Paramétrisation d'un cercle ou d'une droite hyperbolique.
Si l'on pose
{
x
=
cos
θ
=
1
cosh
t
y
=
sin
θ
=
tanh
t
{\displaystyle {\begin{cases}{\begin{aligned}x&=\cos \theta ={\frac {1}{\cosh t}}\\y&=\sin \theta =\tanh t\end{aligned}}\end{cases}}}
x
>
0
{\displaystyle x>0}
θ
{\displaystyle \theta }
(
x
,
y
)
{\displaystyle (x,y)}
(
1
,
0
)
{\displaystyle (1,0)}
t
{\displaystyle t}
géométrie hyperbolique .
Liens externes
Voir aussi
(en) CRC Handbook of Mathematical Sciences 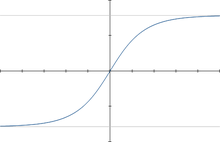









![{\displaystyle ]-\pi /2,\pi /2[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43d9c33ca6a3fbfefb8745778f833ddb0b59893b)




















