Hydrodynamique des particules lissées
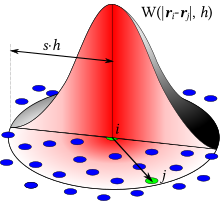
L'hydrodynamique des particules lissées, en anglais Smoothed particle hydrodynamics (SPH), est une méthode de calcul utilisée pour simuler la mécanique des milieux continus, comme la mécanique des solides ou les écoulements de fluides. Elle a été développée par Gingold, Monaghan[1] et Lucy[2] en 1977, initialement pour des problèmes d'astrophysique. Elle a été utilisée dans de nombreux domaines de recherche, incluant l'astrophysique, la balistique, la volcanologie et océanologie. Il s'agit d'une méthode lagrangienne (où les coordonnées se déplacent avec le fluide) sans maillage, et la résolution peut facilement être ajustée en fonction de variables physiques telles que la densité.
Méthodologie
Avantages
- Par construction, la SPH est une méthode sans maillage, ce qui la rend adaptée aux simulation de problèmes caractérisés par une dynamique de frontière complexe, comme les écoulements de surface libre ou les grands déplacements de frontière.
- L'absence de maillage simplifie considérablement l'implémentation du modèle et sa parallélisation, même pour les architectures hautement multicœurs[3],[4].
- La SPH peut être facilement étendue à une grande variété de domaines et hybridée avec d'autres modèles, comme indiqué dans Modélisations physiques.
- Comme discuté dans la section sur la SPH faiblement compressible, la méthode est particulièrement conservative.
- Les simulations SPH ont un coût par nombre de particules nettement inférieur à celui des simulations avec maillage par nombre de maille lorsque la métrique d'intérêt est liée à la densité du fluide (comme, la fonction de densité de probabilité des fluctuations de densité)[5]. Ceci s'explique car la SPH concentre l'effort de résolution là où se situe le besoin.
Limitations
- La définition des conditions aux limites telles que les entrées et sorties[6] et les parois[7] est moins aisée dans la SPH qu'avec les méthodes s'appuyant sur un maillage. En fait, « le traitement des conditions aux limites est certainement l'un des points techniques les plus difficiles de la méthode SPH »[8]. Ce défi est en partie dû au fait que dans la SPH, les particules proches de la frontière changent avec le temps[9]. Néanmoins, les conditions aux limites des murs pour la SPH sont disponibles[7],[9],[10].
- Le coût de calcul des simulations SPH par nombre de particules est considérablement plus élevé que le coût des simulations basées sur la grille par nombre de cellules lorsque la métrique d'intérêt n'est pas directement liée à la densité (mais, par exemple, au spectre d'énergie cinétique)[5]. Par conséquent, en négligeant les problèmes d'accélération par calcul parallèle, la simulation des flux à densité constante (par exemple, l'aérodynamique externe) est plus efficace avec les méthodes à base de maillage.
Exemples
Dynamique des fluides


L'hydrodynamique des particules lissées est de plus en plus utilisée pour modéliser la dynamique des fluides. Cela est dû à plusieurs avantages de la méthode par rapport aux méthodes classiques à base de maillage. Premièrement, la SPH garantit la conservation de la masse sans calcul supplémentaire puisque la masse est incarnée par les particules. Deuxièmement, la SPH calcule la pression à partir des contributions pondérées des particules voisines plutôt qu'en résolvant des systèmes linéaires d'équations. Enfin, contrairement aux techniques à base de maillage lequel doit suivre les limites du fluide, la SPH crée spontanément une surface libre pour les fluides en interaction biphasique puisque les particules représentent le fluide dense (généralement l'eau) et l'espace vide représente le fluide léger (généralement l'air). Pour ces raisons, il est possible de suivre le mouvement du fluide en temps réel avec la SPH . Cependant, les méthodes à base de maillage et la SPH nécessitent toujours la génération d'une géométrie de surface libre pouvant être rendue à l'aide d'une technique de polygonisation telle que les métaballes ou les marching cubes, le splatting ou un plan d'interpolation. Pour la dynamique des gaz, il est plus approprié d'utiliser la fonction noyau elle-même pour produire un rendu de la densité de la colonne de gaz (par exemple, comme cela est fait dans le package de visualisation SPLASH).
Un inconvénient par rapport aux méthodes à base de maillage est le grand nombre de particules nécessaire pour atteindre une même résolution. Dans la mise en œuvre typique des méthodes à base de maillage et de particules SPH, de nombreux voxels ou particules sont utilisés pour remplir des volumes d'eau qui ne sont pas restitués. Mais la précision peut être considérablement plus élevée avec des techniques sophistiquées à base de maillage, en particulier celles recourant à des méthodes particulaires (telles que les ensembles de niveaux de particules), car il est plus facile d'appliquer la condition d'incompressibilité dans ces systèmes. La SPH est de plus en plus utilisée pour la simulation de fluides dans l'animation et les jeux en temps réel où l'interactivité prime sur la précision.
Des travaux récents en SPH appliquée à la simulation de fluides ont permis d'améliorer les performances, la précision et d'élargir les domaines d'application :
- B. Solenthaler, 2009, develops Predictive-Corrective SPH (PCISPH) to allow for better incompressibility constraints[11]
- M. Ihmsen et al., 2010, introduce boundary handling and adaptive time-stepping for PCISPH for accurate rigid body interactions[12]
- K. Bodin et al., 2011, replace the standard equation of state pressure with a density constraint and apply a variational time integrator[13]
- R. Hoetzlein, 2012, develops efficient GPU-based SPH for large scenes in Fluids v.3[14]
- N. Akinci et al., 2012, introduce a versatile boundary handling and two-way SPH-rigid coupling technique that is completely based on hydrodynamic forces; the approach is applicable to different types of SPH solvers [15]
- M. Macklin et al., 2013 simulates incompressible flows inside the Position Based Dynamics framework, for bigger timesteps [16]
- N. Akinci et al., 2013, introduce a versatile surface tension and two-way fluid-solid adhesion technique that allows simulating a variety of interesting physical effects that are observed in reality[17]
- J. Kyle and E. Terrell, 2013, apply SPH to Full-Film Lubrication[18]
- A. Mahdavi and N. Talebbeydokhti, 2015, propose a hybrid algorithm for implementation of solid boundary condition and simulate flow over a sharp crested weir[19]
- S. Tavakkol et al., 2016, develop curvSPH, which makes the horizontal and vertical size of particles independent and generates uniform mass distribution along curved boundaries[20]
- W. Kostorz and A. Esmail-Yakas, 2020, propose a general, efficient and simple method for piecewise-planar SPH wall boundary conditions[10] based on the semianalytical formulation of Kulasegaram et al.[21]
Astrophysique
L'hydrodynamique des particules lissées est particulièrement adaptée aux calculs d'astrophysique théorique du fait d'une résolution adaptative, de la conservation numérique des grandeurs physiques constantes et de sa capacité à simuler des phénomènes couvrant différents ordres de grandeur[22].
Les simulations de formation de galaxies, de formation d'étoiles, de collisions stellaires[23], de supernovae[24] et d'impacts d'astéroïdes font partie des divers champs d'application de la SPH en cosmologie.
La SPH est utilisée pour modéliser les écoulements hydrodynamiques en prenant en compte les effets de la gravité. L'intégration d'autres phénomènes physiques qui peuvent jouer un rôle important, tels que le transfert radiatif et les champs magnétiques, est un domaine de recherche actif chez les astrophysiciens mais au succès mitigé[25],[26].
Mécanique des solides déformables
Libersky et Petschek[27],[28] ont étendu la SPH à la mécanique des solides déformables. Le principal avantage de la SPH dans cette application est la possibilité de traiter une distorsion locale plus importante qu'avec les méthodes à base de maillage. Cette fonctionnalité a été exploitée dans de nombreuses applications en mécanique : formage de métaux, impacts, propagation de fissures, rupture, fragmentation, etc.
Un autre avantage important des méthodes sans maillage, dont la SPH, est qu'elles s’affranchissent naturellement des problèmes de dépendance au maillage. En particulier, l'alignement de maillage est associé aux problèmes de fissures et est évité en SPH du fait du support isotrope des fonctions du noyau. Cependant, les formulations SPH classiques souffrent d'instabilités de traction[29] et d'un manque de cohérence[30]. Au cours des dernières années, différentes corrections ont été introduites pour améliorer la précision de la solution SPH, conduisant au RKPM par Liu et al.[31]. Randles et Libersky[32] ainsi que Johnson et Beissel[33] ont tenté de résoudre le problème de cohérence dans leur étude des phénomènes d'impact.
Dyka et al.[34],[35] et Randles et Libersky[36] ont introduit l'intégration des points de contrainte dans la SPH et Ted Belytschko et al.[37] ont montré que la technique du point de contrainte supprime l'instabilité due à des modes singuliers parasites, tandis que les instabilités de traction peuvent être évitées en utilisant un noyau lagrangien. De nombreuses autres études récentes se trouvent dans la littérature consacrée à l'amélioration de la convergence de la méthode SPH.
Approche numérique
Modélisations physiques
Hydrodynamique
Approche faiblement compressible
Modélisation de la viscosité
Voir aussi
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Smoothed-particle hydrodynamics » (voir la liste des auteurs).
- R.A. Gingold et J.J. Monaghan, « Smoothed particle hydrodynamics: theory and application to non-spherical stars », Mon. Not. R. Astron. Soc., vol. 181, no 3, , p. 375–89 (DOI 10.1093/mnras/181.3.375, Bibcode 1977MNRAS.181..375G)
- L.B. Lucy, « A numerical approach to the testing of the fission hypothesis », Astron. J., vol. 82, , p. 1013–1024 (DOI 10.1086/112164, Bibcode 1977AJ.....82.1013L)
- Takahiro Harada, Seiichi Koshizuka et Yoichiro Kawaguchi « Smoothed particle hydrodynamics on GPUs » ()
— « (ibid.) », Computer Graphics International, , p. 63–70 - Alejandro Crespo, Jose M. Dominguez, Anxo Barreiro, Moncho Gomez-Gesteira et Benedict D. Rogers, « GPUs, a new tool of acceleration in CFD: efficiency and reliability on smoothed particle hydrodynamics methods », PLOS One, vol. 6, no 6, , e20685 (PMID 21695185, PMCID 3113801, DOI 10.1371/journal.pone.0020685, Bibcode 2011PLoSO...620685C)
- Price, D. J., « Smoothed Particle Hydrodynamics: Things I wish my mother taught me », Advances in Computational Astrophysics: Methods, vol. 453, , p. 249 (Bibcode 2012ASPC..453..249P, arXiv 1111.1259)
- « The Smoothed Particle Hydrodynamics Method vs. Finite Volume Numerical Methods », (consulté le )
- Adami, S. and Hu, X. Y. and Adams, N. A.., « A generalized wall boundary condition for smoothed particle hydrodynamics », Journal of Computational Physics, vol. 231, no 21, , p. 7057–7075 (DOI 10.1016/j.jcp.2012.05.005, Bibcode 2012JCoPh.231.7057A)
- Shadloo, M. S. and Oger, G. and Touze, D. L.., « Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges », Computers and Fluids, vol. 136, , p. 11–34 (DOI 10.1016/j.compfluid.2016.05.029)
- Fraser, K.and Kiss, L. I. and St-George, L., « A generalized wall boundary condition for smoothed particle hydrodynamics », 14th International LS-DYNA Conference,
- Kostorz, « A semi-analytical boundary integral method for radial functions with application to Smoothed Particle Hydrodynamics », Journal of Computational Physics, vol. 417, (DOI 10.1016/j.jcp.2020.109565)
- (en) Barbara Solenthaler et Renato Pajarola, « Predictive-Corrective Incompressible SPH », ACM Transactions on Graphics, vol. 29, no 3 doi=10.1145/1576246.1531346,
- Imhsen, « Boundary handling and adaptive time-stepping for PCISPH », Workshop on Virtual Reality Interaction and Physical Simulation VRIPHYS,
- Bodin, « Constraint Fluids », IEEE Transactions on Visualization and Computer Graphics, vol. 18, no 3, , p. 516–26 (PMID 22241284, DOI 10.1109/TVCG.2011.29, lire en ligne)
- (en) Hoetzlein, « Fluids v.3, A Large scale, Open Source Fluid Simulator », sur github.com,
- Akinci, « Versatile Rigid-Fluid Coupling for Incompressible SPH », ACM Transactions on Graphics, vol. 31, no 4, , p. 1–8 (DOI 10.1145/2185520.2185558)
- Macklin, « Position Based Fluids », ACM Transactions on Graphics, vol. 32, no 4, , p. 1 (DOI 10.1145/2461912.2461984)
- Akinci, « Versatile Surface Tension and Adhesion for SPH Fluids SPH », ACM Transactions on Graphics, vol. 32, no 6, , p. 1–8 (DOI 10.1145/2508363.2508395, CiteSeerx 10.1.1.462.8293)
- Jonathan P. Kyle et Elon J. Terrell, « Application of Smoothed Particle Hydrodynamics to Full-Film Lubrication », Journal of Tribology, vol. 135, no 3, (DOI 10.1115/1.4024708)
- Mahdavi and Talebbeydokhti, « A hybrid solid boundary treatment algorithm for smoothed particle hydrodynamics », Scientia Iranica, Transaction A, Civil Engineering, vol. 22, no 4, , p. 1457–1469 (lire en ligne)
- International Journal for Numerical Methods in Fluids, « Curvilinear smoothed particle hydrodynamics », International Journal for Numerical Methods in Fluids, vol. 83, no 2, , p. 115–131 (DOI 10.1002/fld.4261, Bibcode 2017IJNMF..83..115T)
- Kulasegaram, « A variational formulation based contact algorithm for rigid boundaries in two-dimensional SPH applications », Computational Mechanics, vol. 33, no 4, , p. 316–325 (DOI 10.1007/s00466-003-0534-0)
- Daniel J Price, « Astrophysical Smooth Particle Hydrodynamics », New Astron.rev, vol. 53, nos 4–6, , p. 78–104 (DOI 10.1016/j.newar.2009.08.007, Bibcode 2009NewAR..53...78R, arXiv 0903.5075)
- Stephan Rosswog, « SPH Methods in the Modelling of Compact Objects », Living Rev Comput Astrophys, vol. 1, no 1, , p. 1 (DOI 10.1007/lrca-2015-1, Bibcode 2015LRCA....1....1R, arXiv 1406.4224)
- Daniel J Price, Gabriel Rockefeller et Michael S Warren, « SNSPH: A Parallel 3-D Smoothed Particle Radiation Hydrodynamics Code », Astrophys. J., vol. 643, , p. 292–305 (DOI 10.1086/501493, arXiv astro-ph/0512532)
- « Star Formation with Radiative Transfer »
- [PDF] Smoothed Particle Hydrodynamics and Magnetohydrodynamics
- L.D. Libersky et A.G. Petschek, Smooth Particle Hydrodynamics with Strength of Materials, Advances in the Free Lagrange Method, vol. 395, , 248–257 p. (ISBN 978-3-540-54960-4, DOI 10.1007/3-540-54960-9_58)
- L.D. Libersky, A.G. Petschek, A.G. Carney, T.C. Hipp, J.R. Allahdadi et F.A. High, « Strain Lagrangian hydrodynamics: a three-dimensional SPH code for dynamic material response », J. Comput. Phys., vol. 109, no 1, , p. 67–75 (DOI 10.1006/jcph.1993.1199, Bibcode 1993JCoPh.109...67L)
- J.W. Swegle, D.A. Hicks et S.W. Attaway, « Smooth particle hydrodynamics stability analysis », J. Comput. Phys., vol. 116, no 1, , p. 123–134 (DOI 10.1006/jcph.1995.1010, Bibcode 1995JCoPh.116..123S)
- T. Belytschko, Y. Krongauz, J. Dolbow et C. Gerlach, « On the completeness of meshfree particle methods », Int. J. Numer. Methods Eng., vol. 43, no 5, , p. 785–819 (DOI 10.1002/(sici)1097-0207(19981115)43:5<785::aid-nme420>3.0.co;2-9, Bibcode 1998IJNME..43..785B, CiteSeerx 10.1.1.28.491)
- W.K. Liu, S. Jun et Y.F. Zhang, « Reproducing kernel particle methods », Int. J. Numer. Methods Eng., vol. 20, nos 8–9, , p. 1081–1106 (DOI 10.1002/fld.1650200824, Bibcode 1995IJNMF..20.1081L)
- P.W. Randles et L.D. Libersky, « Recent improvements in SPH modelling of hypervelocity impact », Int. J. Impact Eng., vol. 20, nos 6–10, , p. 525–532 (DOI 10.1016/s0734-743x(97)87441-6)
- G.R. Johnson et S.R. Beissel, « Normalized smoothing functions for SPH impact computations », Int. J. Numer. Methods Eng., vol. 39, no 16, , p. 2725–2741 (DOI 10.1002/(sici)1097-0207(19960830)39:16<2725::aid-nme973>3.0.co;2-9, Bibcode 1996IJNME..39.2725J)
- C.T. Dyka et R.P. Ingel, « An approach for tension instability in Smoothed Particle Hydrodynamics », Comput. Struct., vol. 57, no 4, , p. 573–580 (DOI 10.1016/0045-7949(95)00059-p)
- C.T. Dyka, P.W. Randles et R.P. Ingel, « Stress points for tension instability in SPH », Int. J. Numer. Methods Eng., vol. 40, no 13, , p. 2325–2341 (DOI 10.1002/(sici)1097-0207(19970715)40:13<2325::aid-nme161>3.0.co;2-8, Bibcode 1997IJNME..40.2325D)
- P.W. Randles et L.D. Libersky, « Normalized SPH with stress points », Int. J. Numer. Methods Eng., vol. 48, no 10, , p. 1445–1462 (DOI 10.1002/1097-0207(20000810)48:10<1445::aid-nme831>3.0.co;2-9, Bibcode 2000IJNME..48.1445R)
- T. Belytschko, Y. Guo, W.K. Liu et S.P. Xiao, « A unified stability analysis of meshless particle methods », Int. J. Numer. Methods Eng., vol. 48, no 9, , p. 1359–1400 (DOI 10.1002/1097-0207(20000730)48:9<1359::aid-nme829>3.0.co;2-u, Bibcode 2000IJNME..48.1359B)
- [1] J.J. Monaghan, "An introduction to SPH", Computer Physics Communications, vol. 48, pp. 88-96, 1988.
- [2] Hoover, W. G. (2006). Smooth Particle Applied Mechanics, World Scientific.
Liens externes
- David Le Touzé, CFM 2019, La méthode SPH pour les écoulements à surface libre complexe
- Première simulation SPH de la formation des étoiles
- SPHERIC (SPH European Research Interest Community)
Logiciels
- SPH-flow
- « FLUIDS v.1 » (version du sur Internet Archive)
- GADGET
- SPLASH
- SPHysics
- Physics Abstraction Layer
- Phun
