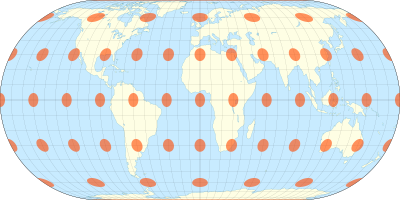
Projection Eckert IV

Crédit image:

Strebe

licence CC BY-SA 3.0 🛈

Crédit image:

Justin Kunimune

licence CC BY-SA 4.0 🛈

La projection Eckert IV est une projection du globe pseudo cylindrique de surface égale présenté par Max Eckert en 1906^[1]. La longueur de la ligne polaire est la moitié de celle de l'équateur, et les lignes de longitude sont des portions d'ellipses.

C'est la projection utilisée dans l'émission Le Dessous des cartes^[2] d'Arte.

Étant donnés le rayon de la sphère R, le méridien central λ₀ et un point de latitude ${\displaystyle \varphi }$ et longitude λ, les coordonnées planes x et y peuvent être calculées en utilisant les formules suivantes :

${\displaystyle x={\frac {2}{\sqrt {4\pi +\pi ^{2}}}}R\,(\lambda -\lambda _{0})(1+\cos \theta )\approx 0.4222382\,R\,(\lambda -\lambda _{0})(1+\cos \theta )}$,

${\displaystyle y=2{\sqrt {\frac {\pi }{4+\pi }}}R\sin \theta \approx 1.3265004\,R\sin \theta }$,

où ${\displaystyle \theta }$ se calcule à partir de l'équation: ${\displaystyle \theta +\sin \theta \cos \theta +2\sin \theta =\left(2+{\frac {\pi }{2}}\right)\sin \varphi }$.

θ peut être calculé numériquement en utilisant la méthode de Newton^[3].

${\displaystyle \theta =\arcsin \left[y{\frac {\sqrt {4+\pi }}{2{\sqrt {\pi }}R}}\right]\approx \arcsin \left[{\frac {y}{1.3265004\,R}}\right]}$

${\displaystyle \varphi =\arcsin \left[{\frac {\theta +\sin \theta \cos \theta +2\sin \theta }{2+{\frac {\pi }{2}}}}\right]}$

${\displaystyle \lambda =\lambda _{0}+x{\frac {\sqrt {4\pi +\pi ^{2}}}{2R(1+\cos \theta )}}\approx \lambda _{0}+{\frac {x}{0.4222382\,R\,(1+\cos \theta )}}}$

• Projections cartographiques
• Projection Eckert II
• Projection Eckert VI

• Page sur le site EPSG (code 54012)
• projection Eckert IV chez Mathworld

• Portail de la cartographie